Considere a região limitada pelas curvas , pelo eixo e pela reta .
Faça um esboço da região .
Escreva uma única integral que expresse a área da região . Não precisa calcular a integral.
Calcule o volume do sólido obtido pela rotação da região em torno do eixo .
Passo 1
Começamos determinando a(s) interseção(ões) dos gráficos. Igualando as funções teremos:
Repara no seguinte, esse cara do pode ser colocado com um produto notável mais prático:
Trazendo isso para igualdade de antes:
Fazendo Bhaskara com o veremos que ele não tem raízes. Assim, o único ponto onde essa igualdade é verdade é quando
Esse será o ponto de interseção, o ponto
Passo 2
O gráfico de fica mais ou menos assim:
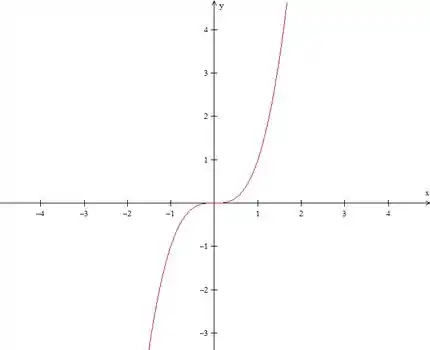
Invertendo ele (multiplicando por ) e descendo ele em unidade (subtraindo ), teremos o gráfico de :
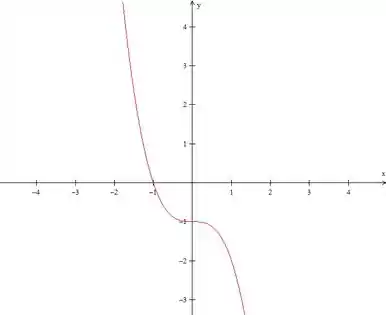
Agora adicionamos a reta e fechamos a região com o eixo (eixo ):
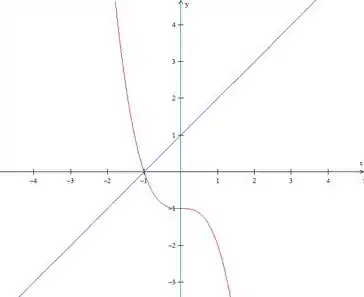
Nossa região é esta acima do , em vermelho, abaixo da reta , em azul, e ao lado do eixo , em verde.
Passo 3
A integral pode ser escrita como a diferença entre a função de cima, , pela função de baixo, , indo do limite inferior, a interseção em , até o limite superior, no eixo , com .
Logo, ficará assim:
Passo 4
Esse volume pode ser achado pelo método das cascas cilíndricas.
O nosso raio será dado pela distância da casca até o eixo, ou seja, .
A altura das cascas terá a diferença entre as funções:
Os limites de integração vão da interseção até o ponto onde a região acaba, ou seja, e .
Dessa maneira, aplicamos a fórmula das cascas cilíndricas: