A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
d., , ; em torno do eixo y.
Passo 1
Fala turminha beleza? Bora lá! A maior dificuldade dessa questão tá na gente conseguir imaginar como ficaria o gráfico dessa questão. Temos isso aqui:
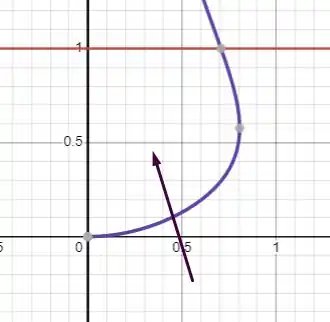
Passo 2
Beleza, agora vamos armar nossa integral. Pra o volume da nossa região em torno do eixo y, temos:
Vamos resolver ela pelo método da substituição. Os limites de integração vai ser justamente 0 e 1, valores que limitam a região do gráfico.
Passo 3
Por fim vamos calcular a integral. Bem tranquila, saca só:
Adotaremos . Portanto nossa integral fica assim:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em