Considere a região delimitada pelas curvas , ,
- Esboce a região .
- Escreva a integral, ou soma de integrais, que determina(m) o volume sólido obtido pela rotação da região acima ao redor do eixo .
- Calcule o volume do sólido do item acima.
Passo 1
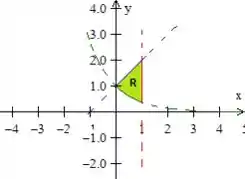
Letra a) então, para a gente começar esse item, é legal a gente começar entendendo quem são essas curvas aí, certo?
Bem, a primeira delas, é uma reta paralela ao eixo que corta o , dessa forma aqui:
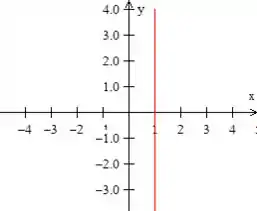
, também é uma reta, mas que passa em quando e quando , dessa forma
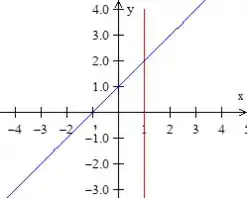
Quanto a última, , ela está com o expoente negativo, portanto é a exponencial só que decrescendo, ou seja:
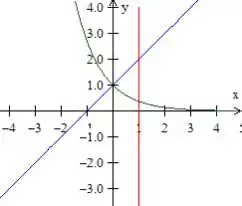
A região delimitada por elas é justamente essa pedacinho aí
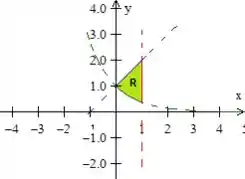
Passo 2
Letra b) Como queremos uma rotação dessa região em torno do eixo , a gente pode tentar encontrar a integral do volume pelo método das cascas cilíndricas, se lembra dele?
Bem, a fórmula é essa daqui, oh:
Ok! Mas no nosso caso quem são esses limites de integração e ?
é o limite inferior da região em , ou seja, é o menor valor que assume na região, portanto o é o valor máximo de que no caso é , ou seja .
Bem, essa e aí uma representa a função que está por cima, e a outra... a que está por baixo, sacou?
Ou seja, no nosso caso, temos que a função que está por cima é a reta e a de baixo é a exponencial
Substituindo tudo...
Passo 3
Letra c) Bem, integral montada, é só cair no abraço e resolver, bora?
Multiplicando tudo ali, teremos...
Como a integral da soma é a soma das integrais...
As duas primeiras integrais, saem direto, mas a última vai exigir um pouco mais da nossa atenção. Mas vamos começar pelas duas primeiras...
Passo 4
Integrando esse polinômios
Substituindo os limites de integração...
Passo 5
Vamos agora para aquela última integral que compõe o volume
Nessa integral podemos pensar em fazer uma integração por partes, ou seja
Vamos tomar o para derivar (porque aí ele desaparece, e o para integrar, lembrando que a integral dele é
Aplicando na fórmula de integração por partes...
Comparando os termos que a gente tem
Passando esse menos para dentro da integral
Essa integral aí, como já vimos, é
Aplicando os limites da definida...
Substituindo os limites...
Passo 6
Voltando para o volume
Resposta
Letra a)
Letra b)
Letra c)