Nos seguintes itens determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados.
b) A região delimitada por , , em torno
(i) da reta
(ii) da reta .
Passo 1
Fala turminha beleza? Bora lá! Primeiro passo é construir a região de acordo com o que ele pede. Temos portanto:
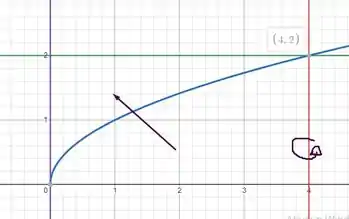
Passo 2
Show, agora vamos usar a imaginação. Ao rotacionar, essa figura vai formar uma espécie de cilindro com uma das faces oca, em um formato irregular mas que iremos calcular o volume. Portanto,
Pra o volume do cilindro, fazemos:
Passo 3
Para o volume oco, primeiro transformaremos a curva que delimita a nossa região. Isso porque como estamos rotacionando em torno do eixo x, precisamos de uma f(x), e não uma f(y) como ele nos entrega.
Agora indo pra integral, temos:
Resolvendo ela, temos:
Sabemos que o volume que a gente quer é igual a diferença desses volumes:
Passo 4
Pra o item ii), temos uma situação diferente. Temos a seguinte rotação:
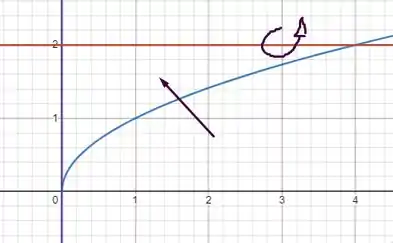
Como agora ela rotaciona em função de x, não precisamos converter fórmula. Portanto, a integral fica (também delimitada pelos mesmos intervalos do item (i)):
Resolvendo ela: