Cálculo de Volumes através de Integrais
Determine o volume do sólido obtido pela rotação, em torno da reta , da região
Passo 1
Vamos começar desenhando a região e tentando definir de que área ele está tratando:
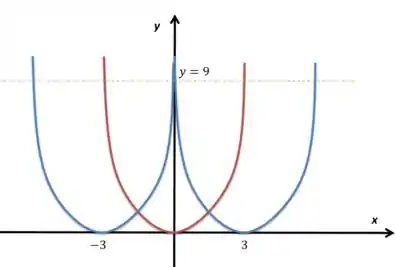
Bom, se você for procurar entender o espaço onde e , ficaríamos com a região dentro do vermelho (acima da linha vermelha) e abaixo da azul:
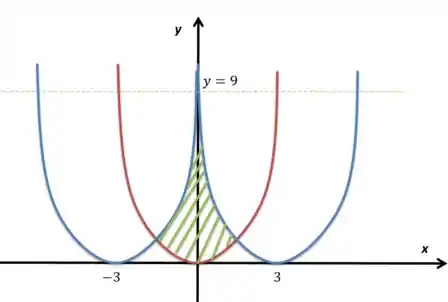
Essa região em verde é a que procuramos. Se trabalharmos as igualdades da parte vermelha com a parte azul da direita temos
E achamos
Se fizermos a outra igualdade, dessa vez da vermelha com a parte azul da esquerda temos
E achamos
A região que está girando vai ser separada em duas parte, uma a direita do eixo e uma a esquerda do eixo . A da direita vai ser o giro do menos o do no eixo , onde vamos ter indo de à .
A partira daí fazemos, no mesmo eixo, giro do menos o do , com entre e . Podemos então armar a operação:
Por simetria, podemos calcular só de um lado e multiplicar por , ou seja: