Cálculo de Volume através de Integrais
Considere a região delimitada pela parábola e pela reta .
Esboce a região
Considere o sólido obtido pela rotação da região ao redor da reta . Escreva uma integral que calcule o volume de .
Calcule o Volume de .
Passo 1
Temos que a expressão da parábola pode ser melhor aberta por:
As raízes serão, para facilitar no seu desenho, aproximadamente e :
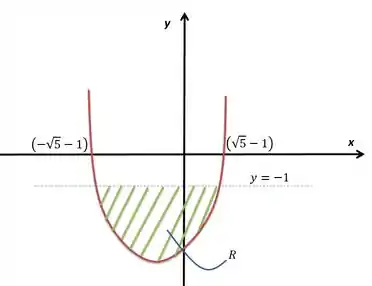
Lembrando que esse é apenas um esboço para dar uma noção geral.
Passo 2
Refiz o desenho adicionando o eixo de rotação para o volume pedido:
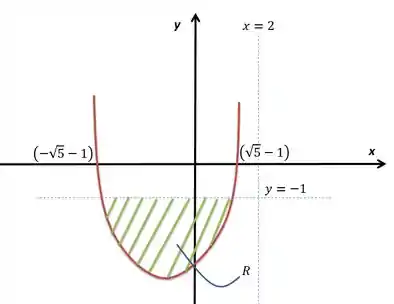
O método mais prático de fazer esse cálculo é através de cascas cilíndricas. Nesse caso, podemos dizer que a altura do cilindro será a distância da parábola até , ou seja
Para o raio, temos que ele valerá a distância horizontal de um ponto qualquer até um ponto na reta na mesma altura, ou seja, será a seguinte diferença:
Assim, nossa integral, que se estende no intervalo dos dois pontos onde encontra :
Terá sua integral dada por:
Passo 3
Agora é só resolver: