Seja a região delimitada pelas curvas e
- Esboce a região
- Escreva a integral, ou soma de integrais, que determina(m) o volume do sólido obtido pela rotação da região acima ao redor da reta
- Calcule o volume da sólido do item acima.
Passo 1
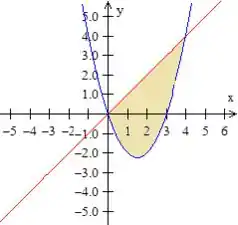
Letra a) Pow, nesse tipo de exercício, ajuda muito se antes a gente entender quem são e como essas duas curvas.
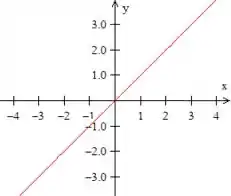
Bem, podemos identificar que a primeira curva é aquela reta passando pela origem
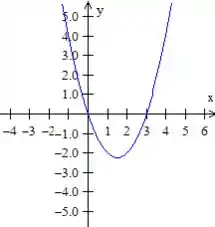
Quanto a curva é uma parábola que passa pela origem e o ponto quando se anula
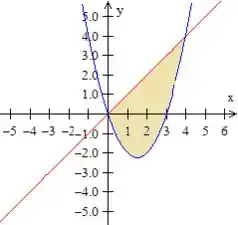
A junção dessas duas curvas terá a região amarela
Passo 2
Letra b) Pow, a gente vai girar a curva em torno da reta . Primeiramente, perceba que essa reta é uma reta paralela ao eixo , dessa forma aqui
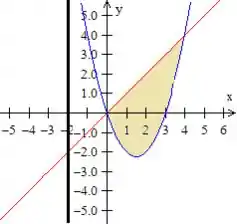
Como essa reta está paralela ao eixo , é super aconselhável que façamos pelo método das casacas cilíndricas, percebeu?
Então vamos recordar a fórmula desse método:
Eu sei! Fórmula gigante, neh? Calma que vamos recordar passo a passo quem são esses termos, bele?
Vamos começar por esses limites loucos aí, e
Passo 3
Então, e são os limites que assume dentro dessa região, e para determinar isso, a gente vai olhar para a interação matemática dessas duas curvas, ou seja, vamos descobrir quem são aqueles dois pontos de intersecção. Veja só
Basta então resolver esse sisteminha com as duas curvas e pronto!
Substituindo o de cima na de baixo
colocando o em evidência...
logo, ou ou
Logo, os dois pontos são como poderíamos imaginar pelo gráfico o e o
Passo 4
Então a gente tem que
Agora, o que significa esse termo ?
Bem, o é a reta que vamos girar a região, portanto
Passo 5
Tamo montando a nossa integral de pouco a pouco, percebeu? :D
Só falta agora a gente falar quem é essa e essa .
Bem, pela teoria dessa matéria, a gente tem que a é a função que está por cima (no nosso caso é a reta)
e a , é a função que está por baixo, portanto
Então a gente pode concluir que
Dando uma arrumada na casa :D
Prontinho! Integral que resolve a nossa vida!
Passo 6
Letra c) Bem, agora é só resolver a integral acima
Multiplicando esses termos entre parênteses
Calculando a integral de cada um desse termo aí
Substituindo esses limites
Resposta
Letra a)
Letra b)
Letra c)