Cálculo de Volumes através de Integrais
Encontre o volume gerado pela rotação da região limitada
em torno da reta .
Passo 1
O probleminha nos dá uma região limitada por:
Como você pode perceber, ainda não sabemos muito bem qual é a região a ser rotacionada em torno de . Por isso, vamos começar esboçando a região a partir do esboço das curvas.
Passo 2
Vamos começar estudando o comportamento da função .
Interseção com o eixo :
Interseção com o eixo
Repare que quando , . Logo, a região limitada está entre e .
Primeira derivada:
Segunda derivada:
Esboço da função:
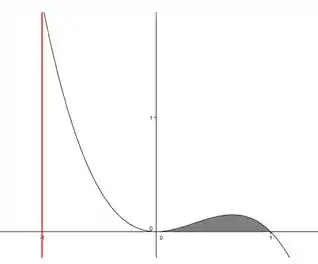
É conveniente usarmos o método das cascas cilíndricas (já que não podemos calcular pelo método das seções transversais):
Passo 3
Logo:
OBS:
Nesse problema, usamos o método das cascas cilíndricas.
Você deve usá-lo sempre que for muito difícil usar o método das seções transversais.
Por exemplo: como acharíamos o raio interno e externo do sólido? Não dá! Pois só temos uma função, e não duas.