12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
h)
Passo 1
Falaaa... Belezinha?
Essa questão está pedindo pra usar o método da casca pra determinar o volume do sólido de revolução, em torno do eixo , da região limita pela curva e as retas e .
Mas que método da casca é esse? É aquele da casca cilíndrica.
Com esse método vamos achar o volume do sólido a partir de algum cilindro mais genérico que esteja inscrito no sólido.
E usar a equação:
Ta... um monte de palavra bonita, né? Mas como fazemos isso na prática?
Passo 2
Primeira coisa que vamos fazer é esboçar essas duas curvas pra achar qual é essa bendita região delimitada.
Esboçando as retas:
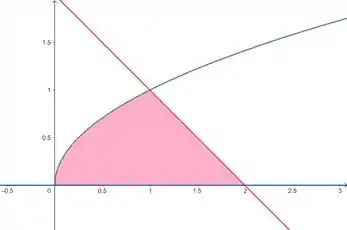
Vamos aproveitar e já calcular esses três pontos de intersecção. Pra isso, igualamos as equações da curva e retas, duas a duas.
Primeiro as duas primeiras retas. ( e )
E, substituindo na equação, x
Agora a primeira e a terceira. ( e )
Elevando os dois lados ao quadrado, pra ficar mais fácil de resolver:
Resolvendo essa equação temos dois valores: e .
Substituindo na equação , temos e , respectivamente.
E substituindo na equação temos e , respectivamente.
ATENÇÃÃOO...
Repara que achamos valores diferentes ( e ), maas era pra ser igual porque a gente igualou as equações. Isso acontece porque a gente elevou ao quadrado pra resolver a equação, mas fazendo isso consideramos a parte de baixo da parábola também, que seria . Então desconsideramos esse ponto.
Fica só o ponto e .
E, por último, a segunda e a terceira. ( e )
Substituindo na segunda:
Passo 3
Agora vamos fazer aparecer o tal do cilindro.
Como a rotação é em torno do eixo , vamos tração uma “linha”, de largura , paralela ao eixo ligando a curva e a reta que delimitam a área. Esse vai ser o lado do nosso cilindro.
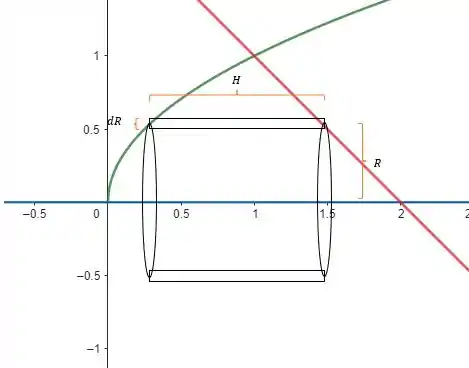
Daí podemos já dizer quem é quem.
Como escolhemos uma paralela ao eixo para traçar o lado do cilindro, então .
E a espessura da linha é .
Já, para , temos que é apenas entre os valores de e . Mas estamos trabalhando com , então e . Então:
Passo 4
Agora é só jogar tudo na equação:
Ahhh... mas faltam os limites de integração, né?
No final do passo 2 achamos pontos importantes. Daí podemos ver, então que varia entre 0 e 1. Então:
Resolvendo:
Boaaa... terminamos essa. Vamos pra próxima?