Exercícios Resolvidos de Cascas Cilíndricas

Exercício 26 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Seja a região delimitada pelas curvas ,

Esboce a região

Determine a área da região

Calcule o volume do sólido obtido pela rotação desta região ao redor da reta

Passo 1

Vamos um por um: temos uma parábola , com vértice em . Somada a essa parábola, aparece uma reta , que delimita região com a parábola.

Os pontos de encontro delas serão:

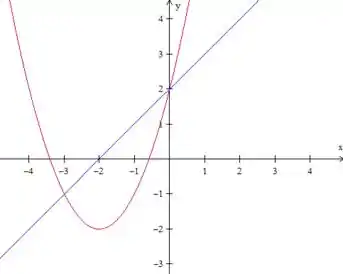
Juntando tudo, ficamos assim, com essa região de até :

Passo 2

Olhando o gráfico, a gente vê que podemos achar essa área como a integral de menos de até .

Logo,

Passo 3

Resolvendo a integral

Passo 4

Vamos utilizar o método das cascas cilíndricas. Usando como altura a própria diferença entre as duas funções, a reta e a parábola:

O raio será dado pelo módulo de somado a . Nesse caso, como temos , temos:

A fórmula da casca cilíndrica é:

Passo 5

Resolvemos a integral agora:

Resposta

Exercícios de Livros Relacionados

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B

Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em