Considere a região plana definida por:
(a.1) Esboce a região plana
(a.2) Escreva a área da região como uma integral na variável
(a.3) Escreva a área da região como uma soma de integrais na variável
Seja um sóldio de revolução obtido pela rotação da região em torno do eixo
(b.1) Utilizando o Método de Discos, escreva o volume de como uma integral na variável
(b.2) Utilizando o Método de Cascas Cilíndricas, escreva o volume de como uma soma de integrais na variável
(b.3) Calcule o volume de pelo método que preferir
Passo 1
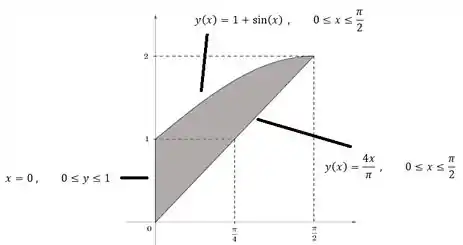
(a.1) Esboçando a região
Essa questão vai ser longa porque todos os subitens estão conectados então pega lá seu café e vamo que vamo. Primeiro, vamos olhar a região do enunciado e seus limites: em é limitado por números e em por funções. Os limites de vão ser:
Então nossa região vai com certeza estar entre essas duas retas verticais, beleza?
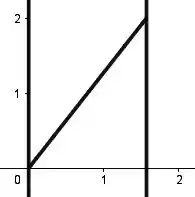
Show, agora vamos falar das limitações de . Por baixo, a limitação é . Opa, isso ai é uma reta! Só desenhar então uma reta saindo da origem, de inclinação . Mas ó, só vamos desenhar a parte dela que fica dentro da região acima. Vamos ter então:
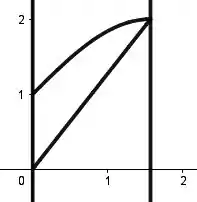
E por cima, é limitado por , que é uma função com “cara de onda” por causa do . Vamos desenhar por cima dessa reta então a ondinha:
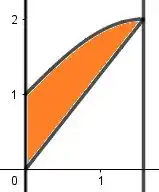
A nossa região vai ser então:
Passo 2
(a.2) Escreva a área da região como uma integral na variável
A gente já ta careca de saber que a integral de uma função nada mais é do que a área abaixo da curva, dados os limites de integração, não é? Então basta a gente deixar bem claro quem é quem no nosso esboço do gráfico. Vamos ter então:
Um cuidado aqui galera, da uma olhada:
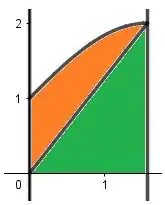
A área abaixo de é a área laranja somada com a área verde, enquanto a área abaixo de é só a verde. Como queremos só a área laranja, temos que fazer:
Mas como o enunciado pediu uma integral só:
Passo 3
(a.3) Escreva a área da região como uma integral na variável
Isso aqui colocaram só pra complicar, mas relaxa que a gente tira de letra. Pra respondermos isso, vamos primeiro “deitar” nossa região . Quando a gente põe a região deitada, invertemos todas as funções. Dá uma olhada:
Graficamente, temos:
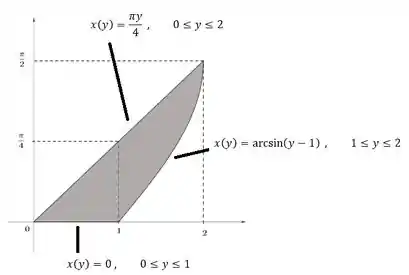
E agora é moleza porque pra calcular essa área a gente usa a mesma ideia que usamos pra área em função de . Então ficamos com:
- A áre do ponto 0 até o 1 (área do triângulo da pontinha):
- A área do ponto 1 até 2: é a área abaixo da reta menos a área por baixo do arcoseno...
- Volume abaixo da reta:
- Volume abaixo do arcoseno (Curvinha de 1 até 2):
Então a área da figura total é a soma das duas partes:
Ou, tirando dos parênteses...
Como as duas primeiras integrais são as mesmas e a função é contínua... Podemos colocar em uma integral só integrando direto de a , por propriedade da integral, se lembra?...
Passo 4
(b.1) Utilizando o Método de Discos, escreva o volume de como uma integral na variável
Chegamos na metade da questão em! Se seu café acabou a essa altura, pega mais um pouco pra te dar um gás. Aqui temos que escrever sem resolver o volume do sólido de revolução usando o método dos discos.
Vamos lembrar que o sólido é a revolução em torno do eixo da região . Como o método de discos já é feito pensando na revolução nesse eixo, vamos dar uma olhada na região e entender como ela fica:
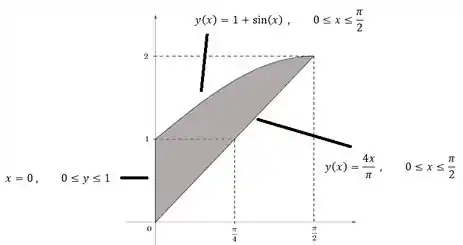
Beleza, tamos duas curvas interessantes aí e cada uma delas gera um sólido diferente. A curva revolucionada gera meio que uma “tigela sem furo”. Mas toda boa tigela precisa de um furo pra por os biscoitos dentro. Esse furo é exatamente o cone que é gerado quando revolucionamos .
Então o nosso sólido é uma tigela com furo e pra gente calcular o volume dela, vamos ter que tirar o volume do furo da tigela sem furo. Sendo assim, usando o método de discos para cada uma das curvas, vamos ter
E como o enunciado pede numa integral só:
Passo 5
(b.1) Utilizando o Método das cascas cilíndricas, escreva o volume de como uma soma de integrais na variável
Aqui a gente vai ter uma leve complicaçãozinha mas nada que não demos conta. O método das cascas cilíndricas é pra revolução no eixo , mas nosso enunciado quer no eixo . E agora?
Calma, respira que é tranquilo. Na verdade, já fizemos o que é preciso pra resolver esse problema. Pra usar esse método então, temos que trocar de lado os eixos. E o que é isso se não “deitar” o gráfico e inverter as funções? Pra ficar ainda mais claro:
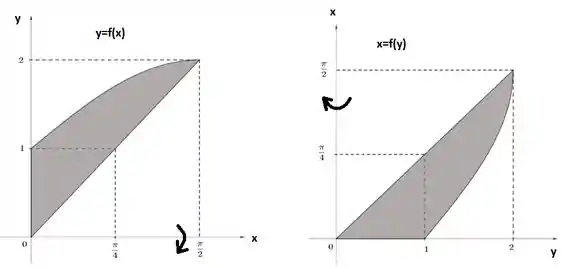
As duas rotações acima são iguais! Então se usarmos as funções inversas no método das cascas cilíndricas, vamos obter o mesmo sólido. Então foca nesse gráfico daqui pra não confundir:
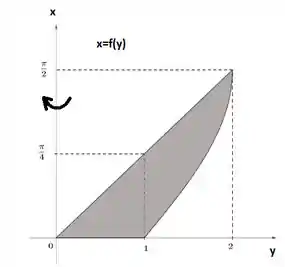
No método das cascas, o volume é dado por...
Veja que temos a integral na variável e não em como usual. Isso está acontecendo porque estamos girando em torno de (como se ele fosse agora a variável dependente, saca?). Repare também que o volume total é o volume que está abaixo da reta menos o pedacinho que está abaixo do arcoseno! Então o volume total é a sobtração dos dois
Logo o volume total do sólido é
Embora o volume está dado pela subtração, isso é uma soma também, pois sempre podemos escrever
Passo 4
(b.3) Calcular o volume por qualquer um dos métodos
Opa, agora é só calcular mesmo. Trabalho braçal infelizmente mas pelo menos estamos chegando ao fim. Vamos lá então, as fórmulas que podemos usar são:
A segunda parece um pouco complicada né? Vamos então com a primeira. Vamos ter:
Ai calculando cada uma das integrais, vamos ter, na primeira:
E pra segunda integral:
Pra terceira integral:
Realizando a substituição simples
Ficamos com:
E pra quarta integral, finalizando:
Juntando tudo:
Ufa, fechamos a questão!
Resposta
(a.1) 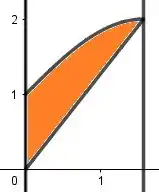
(a.2)
(a.3)
(b.1)
(b.2)
(b.3)