
Passo 1
Entender o problema. Bora fazer uma figurinha para ver o que que esse cara fez:
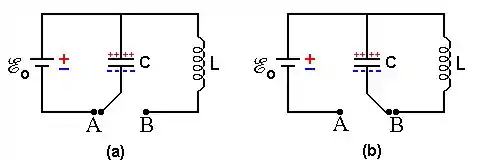
Primeiro o capacitor pegou a carga com a bateria. Depois que ele ficou carregado, a gente mudou a chave de posição e fechou o capacitor em cima do indutor. Isso aí é o clássico circuito LC.
Passo 2
Letra (a). A própria definição de capacitância nos permite achar quem é a carga inicial desse capacitor:
Pois é. A definição de capacitor pode ser resumida como: quantode carga eu gero entre cada plaquinha para cada unidade de carga que eu boto a mais ali?
Passo 3
Letra (b). Quando estamos em ,toda a carga vai para o capacitor. Toda a energia se dirige a ele. Depois disso, a energia vai pro indutor, volta para o capacitor e fica zanzando de lá pra cá.
O que importa aqui é a energia total e, no instante , a energia do capacitor é, de fato, igual a energia total (nem deu tempo ainda de que o indutor pegasse energia).
Então:
Passo 4
Letra (c). Parte 1. Para saber o que acontece com essa energia, como ela fica zanzando de lá pra cá, a partir do instante inicial, temos que escrever a equação diferencial do circuito. Isso se resume a escrever um conjunto de equações e depois juntar todas elas numa coisa só, numa coisa completa, que descreve tudo, ok?
- Equação do capacitor:
- Equação do indutor:
-
Capacitor e indutor estão em série. Logo:
- (a corrente que passar em um é a mesma que passa no outro)
- (parece meio maluco, mas isso acontece porque não tem nenhuma bateria no circuito da figura, depois de girarmos a chave)
Vou aqui escrever as coisas de um jeito mais simplificado beleza? Já estou considerando aqui que as correntes são iguais e os potenciais somam zero, para o capacitor e para o indutor (informação “3”).
Então:
Substituindo em :
Essa equação descreve as oscilações de corrente. Para descrevermos as oscilações de carga, devemos fazer:
Passo 5
Letra (c). Parte 2. Para descrever o comportamento da carga no capacitor, vamos olhar a equação:
A carga no capacitor possui a forma:
Substituindo:
Assim:
Como consideramos que, no instante inicial, , a carga no capacitor se inicia em seu valor máximo, temos . Além disso, como visto no passo 1, a carga máxima vale: .
Dessa forma, a carga do capacitor pode ser descrita por:
Passo 6
Letra (d). A partir do resultado do passo anterior, podemos determinar a corrente elétrica por derivação:
Passo 7
Letra (e). Dessa forma, tanto a corrente quanto a carga (e até mesmo as tensões elétricas do capacitor e do indutor) oscilam com frequência angular:
Resposta
- e