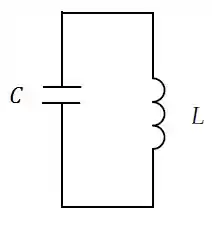
Num circuito , e . No instante , a corrente é de , a carga do capacitor é de e o capacitor está sendo carregado.
- Qual é a energia total do circuito?
- Qual é a carga máxima do capacitor?
- Qual é a corrente máxima?
- Qual é o período de oscilação da corrente no circuito?
- Sabendo-se que a carga do capacitor é dada por , qual o valor de ?
Passo 1
a) Qual é a energia total do circuito?
A energia total do circuito será igual à soma das energias acumuladas no capacitor e no indutor.
Onde:
Logo:
Bom... agora é só substituir os valores e ser feliz.
Substituindo os valores, vamos encontrar o seguinte:
Passo 2
b) Qual é a carga máxima do capacitor?
O capacitor terá carga máxima quando toda a energia do circuito for igual a (quando for igual a zero), logo:
Passo 3
c) Qual é a corrente máxima?
Nesse caso, a corrente máxima passará pelo circuito quando (quando for nulo), logo:
Passo 4
d) Qual é o período de oscilação da corrente no circuito?
A frequência de oscilação é dada por:
Agora podemos calcular o período
Passo 5
e) Sabendo-se que a carga do capacitor é dada por , qual o valor de ?
Voltando no enunciado, ele nos diz que, quando , . Agora o nosso único trabalho é isolar o .
Resposta
a.
b.
c.
d.
e.