Medidas realizadas no circuito em série mostrado na Figura 1 revelaram que e , , , e . Adicionalmente, sabe-se que apenas uma das relações é verdadeira: ou .
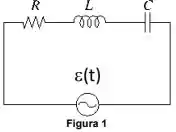
(a) (0,5) Indique, justificando, a relação verdadeira.
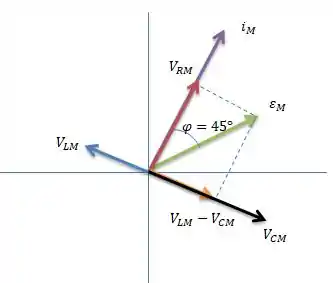
(b) (1,0) Represente o diagrama fasorial para o circuito, de tal forma que os fasores correspondentes a tensões () estejam em escala e que o fasor corrente, a defasagem entre a corrente e a fem estejam representados.
(c) (1,0) Determine os valores de , e .
(d) (0,5) Apresente expressões completas para e
(e) (0,5) O indutor é trocado por outro, com indutância igual a . Os seguintes elementos do circuito permanecem inalterados:, e . Determine a nova capacitância que torna o circuito ressonante, assim como o novo valor de .
Passo 1
Cara, sabemos pela Teoria que o ângulo em um circuito em corrente alternada...
É de tal maneira que...
Onde são as tensões máximas em cima de cada item.
Ou ainda, extraindo a tangente de ambos os lados...
Como (ou ) a tangente dele vai ser igual a ...
Como todas essas tensões máximas (ou tensões de pico) são positivas, para gerar um valor negativo nessa divisão só pode que , assim...
E aí faz sentido a equação .
Passo 2
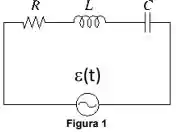
Bem, a gente sempre começa um diagrama fasorial representando a corrente máxima do circuito e a máxima ...
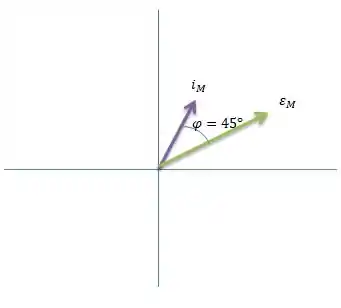
Sendo que o ângulo entre ambos os fasores é sempre o ângulo de defasagem entre a corrente a . No caso, como o enunciado nos disse que , isso significa que a corrente deve estar na frente da tensão (como já representado). Isso também caracteriza um circuito mais capacitivo, por isso a tensão em cima do capacitor é maior, ta ligado?
Enfim, continuando, agora é hora de colocar a tensão em cima do resistor que tem que estar em cima da corrente e deve ser a projeção da ...
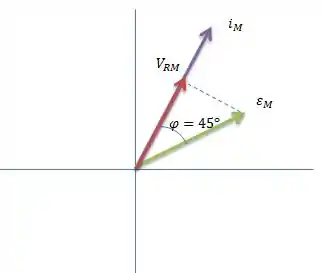
Além disso, como a máxima tensão em cima da tem que ser igual a soma vetorial... , então concluímos que...
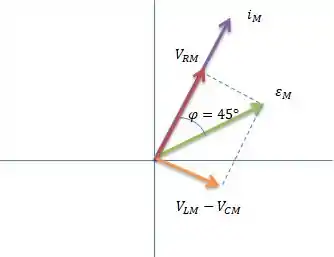
Como o problema nos deu a informação adicional de que , e a tensão do indutor está sempre avante a corrente de e está sempre atrás da corrente de ...
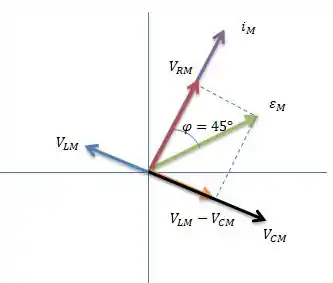
Concluímos que esse é o diagrama fasorial do problema e está em escala
Passo 3
Pelo diagrama fasorial acima podemos falar que...
Além disso, também sabemos que pela Lei de Ohm...
Como a corrente ...
Passo 4
Agora, para encontrar os valores de e , temos primeiro que determinar e . Pelo diagrama Fasorial...
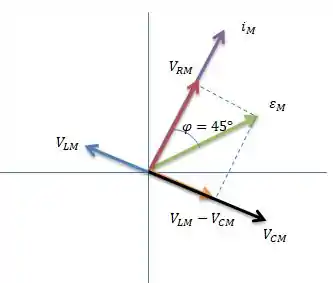
Então...
Só que pelo enunciado ...
Ou em módulo...
E o ...
Pela teoria, sabemos que o equivalente da Lei de Ohm para o indutor é...
E para a capacitância ...
Passo 5
Bem, pela análise do diagrama fasorial...
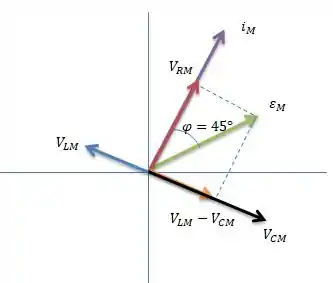
Veja que a tensão do resistor está bem em cima da corrente, então a tensão em cima do resistor vai variar conforme ...
Para o indutor e o capacitor basta somar e subtrair (ou ), mas lembre-se que o indutor está na frente da corrente por então ele é o que soma...
Como todos esses dados já forma encontrados...
Simplificando esses dois últimos...
Passo 6
Cara... Para um circuito Ressonante, temos que ter...
Daí...
Onde é a frequência de ressonância. Como o problema nos pediu para encontrar o valor da capacitância capaz de tornar o sistema ressonante sabendo que permaneceu o mesmo, basta isolar...
O problema nos disse que a indutância nova trocada foi para ou ainda ...
Como ...
Ou ainda, a nova capacitância tem que ser .
Passo 7
Também temos que encontrar o novo valor de . Como o circuito é ressonante, significa que a corrente está em fase com a , isto é agora é (a corrente e a tensão estão juntas). Como...
Então...
Esses dois parâmetros permanecem inalterados, então...
Resposta
Letra A:
Letra B:
Letra C:
Letra D:
Letra E: