Uma estação de rádio FM tem sua transmissão radiofônica na frequência de . Qual deve ser o valor aproximado da indutância que deve ser ligada a um capacitor de para se construir um circuito receptor para esta estação? (Usar
Passo 1
Essa questão é legal, porque a gente pode revisar uma analogia interessante com a mecânica, em particular, a da mecânica envolvida no oscilador harmônico simples, vulgo MHS. Mas, como assim?
Considere o circuito LC de uma única malha abaixo.
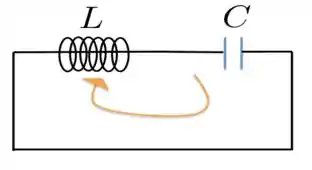
Agora, vamos aplicar a lei de Kirchhoff das malhas considerando o sentido dado pela seta em amarelo na figura acima. Fazendo isso, temos
Agora, recordando um pouco lá do início dos nossos estudos de eletricidade, a gente sabe que uma corrente nada mais é do que o movimento de cargas elétricas, então podemos escrever que a corrente é
Lembrou disso? Se não, a gente está aqui para relembrar isso para você :-). Pega essa equação e substitui naquela que a gente obteve da lei de Kirchhoff e você vai chegar fácil, fácil em
Essa equação te lembra alguma outra do seu passado com a Física 2? Não se preocupe se agora não te vem à cabeça nenhuma lembrança…relaxa…kkk Te ajudo nisso!! Segue pro próxmo passo e a gente vai caminhando para lembrar disso…
Passo 2
Se você trocar por e chamar essa variável de posição de uma determinada partícula de massa presa a uma mola de constante elástica, você vai poder comparar as duas seguintes equações:
em que dá, em ambos os casos, a velocidade angular de oscilação da carga no circuito LC (equação acima à esquerda da seta) e a velocidade angular de oscilação da partícula de massa presa a uma mola de constante elástica (equação acima à direita da seta).
Daí você me pergunta: para quê falar de MHS lá da partícula presa à uma mola e submetida à força de Hooke?
Reposta: para que você tenha uma analogia pronta na cabeça quando o assunto for circuito LC! Se você sabe a solução lá do MHS, você sabe a solução do circuito LC e vice-versa. Ou seja, VOCÊ MATA DOIS TIPOS DE PROBLEMA COM UMA PAULADA SÓ!!!
Passo 3
Bom, mas nosso problema aqui é de eletricidade, né? Então vamos tomar apenas o seguinte
que pode nos dar a frequência natural de oscilação da carga e, portanto, da corrente no circuito da figura. No caso do problema, a gente tem que e também temos a capacitância , sendo . Portanto, substituindo na equação acima (considerando e sabendo que ):
Resposta
Portanto, letra d).