
a)
b)
c)
d)
e)
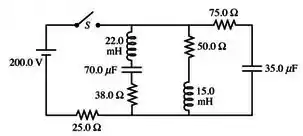
Passo 1
Assim que o interruptor é fechado:
- Os capacitores se comportam como um curto-circuito
- Os indutores se comportam como um circuito aberto
Passo 2
Logo, a corrente circula somente na malha externa. Ou seja: ela sai da fonte de e passa pelos resistores de e , passando pelo capacitor de !
A diferença de potencial no indutor de é igual à DDP em cima do resistor de .
Passo 3
Para calcular essa DDP, vamos começar pelo cálculo da corrente na malha externa:
Passo 4
Logo:
Passo 5
Quando o interruptor fica fechado por muito tempo, a coisa se inverte:
- O capacitor passa a se comportar como um circuito aberto
- O indutor passa a se comportar como um circuito fechado
E aí o percurso da corrente muda: ela passa a circular saindo da fonte de tensão, passando pelo resistor de , pelo indututor de e pelo resistor de
Então, a DDP em cima do capacitor de é igual à DDP em cima do resistor de , já que não há corrente em cima desse capacitor:
Resta calcular a corrente!
Passo 6
E a corrente a gente calcula pela lei de Ohm:
E aí a gente encontra o potencial no capacitor quando o tempo tende ao infinito:
Resposta
Letra (e).