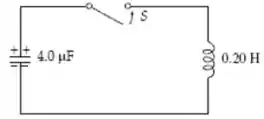
08) Antes do interruptor ser fechado no circuito ilustrado na figura, a ddp nos terminais do capacitor é de . Em algum instante depois de o interruptor ser fechado, a corrente instantânea vale . Qual é o valor da energia armazenada no campo elétrico do capacitor neste instante?
a)
b)
c)
d)
e)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão temos um circuito como descrito na imagem do enunciado.
Inicialmente a chave que liga o capacitor e o indutor está aberta, isolando o capacitor do indutor.
O capacitor está inicialmente carregado e a tensão entre seus terminais é .
Um instante após a chave se fechar, a corrente do circuito vale .
Com apenas essas informações, queremos saber qual é a energia armazenada no campo elétrico do capacitor nesse instante.
Tem ideia de como fazer isso? 🤔🤔
Há duas coisas importantes que vamos precisar para resolver esse problema. Primeiro temos que lembrar quais são as equações que descrevem os valores das energias armazenadas pelo capacitor e indutor.
Para o capacitor, sua energia armazenada é dada por
Já para o indutor, a energia armazenada é dada por
Entendeu essa parte? 😁
O outro ponto importante é que em um circuito não há desperdício de energia, então a energia no circuito é constante e é conservada durante todo o tempo.
Com isso, podemos dizer que a energia inicial do circuito é igual a energia final do circuito.
Agora podemos começar! 😉
Passo 2
Inicialmente a chave está aberta, o capacitor está completamente carregado e o indutor não possui energia.
Assim, podemos dizer que a energia inicial é igual a
Como , podemos afirmar que .
Simplificando
No enunciado foi dito que a tensão no capacitor é de e na imagem do enunciado vemos que a capacitância do capacitor é . Fazendo essas substituições em
Com isso, vemos que a energia inicial do capacitor e do circuito é .
Tranquilo até aqui? 😎
Passo 3
Agora vamos calcular a energia final do circuito sabendo que agora parte da energia foi transferida para o indutor.
Não sabemos qual é a energia final do capacitor, mas podemos obter a energia no indutor dado que a corrente do circuito no momento é e que a indutância do indutor é .
Com a energia final do indutor calculada, podemos igualar e para obter .
Isolando em um lado da equação passando para o outro lado com o sinal trocado, temos
Dessa forma, calculamos que a energia armazenada no campo elétrico do capacitor no momento que a corrente do circuito é é , ou seja, a alternativa correta é a letra b)!
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
b)