UFF – Física 2 – Provas Antigas – VR – 2022.1 – Questão 15
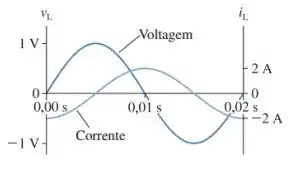
Um indutor em um circuito RLC em série é monitorado por um voltímetro e um amperímetro de forma que o gráfico da corrente e voltagem através dele são visualizados na figura a seguir. Sabendo-se que o circuito encontra-se em ressonância, determine a capacitância do capacitor.
A)
B)
C)
D)
E)
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão temos que determinar a capacitância do capacitor a partir (dica: vamos observar principalmente o período e o pico dos gráficos viu?).
Como trata-se de um circuito ressonante, então a reatância do indutor é igual a do capacitor, ou seja:
Agora vamos utilizar isso como base para podermos encontrar o que queremos!!
Então bora lá!!!
Passo 2
Assim, sendo a tensão do indutor dada por:
Pelos gráficos, vemos que:
E a corrente no indutor é:
Podemos substituir em :
Passo 3
Assim, como queremos apenas o módulo da capacitância , podemos desconsiderar o sinal e, igualando as duas reatâncias, temos:
Entendeu direitinho? Responde aee ;)
Resposta
B)