No circuito ilustrado na figura abaixo, tanto a indutância do indutor, quanto a capacitância do capacitor são alteradas. As alternativas abaixo apresentam as variações na indutância e na capacitância. Assinale aquela que reduzirá a frequência de oscilação da corrente no circuito.
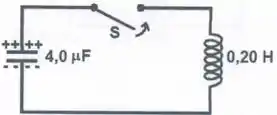
(a) e .
(b) e
(c) e .
(d) e .
(e) e .
Passo 1
A frequência de oscilação é dada por:
logo, reduzirá se aumentar. Dentre as opções, a letra (d) é a que proporciona um aumento de e, consequentemente, uma diminuição de .
Resposta
(d) e .
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.