Antes de o interruptor ser fechado na figura, a ddp nos terminais do capacitor era de . Em algum instante depois do interruptor ser fechado, a corrente instantânea circulando no circuito é de . Qual é o valor da energia armazenada no campo elétrico do capacitor neste instante?
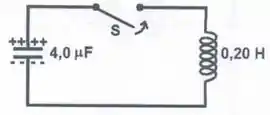
(a)
(b) .
(c) .
(d) .
(e) .
Passo 1
Antes de o interruptor de fechado, a energia total armazenada no capacitor (e no circuito!) é dada por:
Passo 2
Ao fechar o interruptor, a energia no indutor será dada por:
Como a energia se conserva, a energia no capacitor será a energia total inicial, calculada no Passo 1, menos a energia no indutor. Temos:
Resposta
(b) .
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.