Considere o circuito mostrado na figura abaixo, onde o capacitor está inicialmente descarregado. Considere , , , e dados.
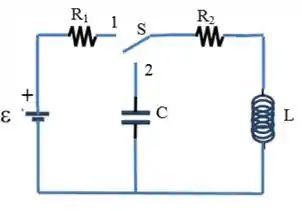
Fase I: A chave é comutada para a posição (). Nestas condições:
Escreva a expressão da corrente no circuito em função do tempo .
Após um tempo muito longo, determine as tensões sobre , e .
Fase II: A chave é comutada para a posição ().
Temos agora um circuito RLC em série onde a corrente pode ser aproximadamenre dada pela seguinte expressão: . determine os três parâmetros desta expressão: , e em função dos dados do problema (, , , e ).
Após um tempo muito longo calcule a energia total dissipada em .
Passo 1
Durante a fase , temos um circuito RL. Para esse tipo de circuito, temos que a corrente varia da seguinte maneira:
Podemos sempre chegar nas equações para corrente usando a lei das malhas, mas é mais fácil decorar essas malditas.
No caso acima, temos que a resistência equivalente é a soma das resistências, tendo em vista que os resistores estão em série, então, a equação da corrente é:
Passo 2
No fim da fase , o indutor se comporta como um fio qualquer sem resistência, e portanto, a d.d.p entre seus terminais é nula, e a corrente no circuito é máxima . Logo, a tensão está dividida entre as duas resistências, usando , temos:
Além disso:
Substituindo nas duas primeiras equações, temos:
Passo 3
Com a chave na posição , temos um circuito RLC, nesse tipo de circuito, a corrente, conforme dito no enunciado é dada pela seguinte expressão:
Precisamos agora determinar , e . Vamos começar com o valor da corrente.
Para , temos que a corrente é , e deve ser igual à corrente no fim da fase , ainda bem que já calculamos isso no item anterior!
Agora, como calculamos o resto?
Nós sabemos lá da teoria que a fórmula da carga no circuito RLC é dada por:
Para calcular a corrente, basta derivar em relação a e chegaremos nisso:
Eu sei! Que coisa gigante e horrorosa, né? Mas existe um bizu que vai nos ajudar a simplificar isso (graças!!!)
Bizu:
onde e .
Considerando e , podemos chegar que a equação da corrente é algo assim:
Comparando com a equação do enunciado , temos que .
No nosso caso:
Finalmente, temos que , para o nosso circuito, temos:
Passo 4
Para determinar a energia dissipada na resistência durante a fase dois, devemos calcular a energia armazenada no indutor durante a fase . Como o capacitor está inicialmente descarregado, somente a energia armazenada no indutor será dissipada no resistor, vamos calcular isso:
Substituindo o valor da corrente, que já calculamos, temos:
Resposta
;