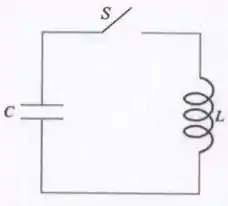
A figura abaixo ilustra um circuito elétrico contendo um capacitor , um indutor e uma chave . Sabe-se que no instante , a chave é fechada, e que nesse instante, o capacitor tem carga elétrica máxima dada por e que a corrente elétrica inicial no circuito é nula . Para tal situação, determine:
- O instante de tempo para o qual a carga armazenada no capacitor se reduz a de sua carga em .
- O instante de tempo para o qual a energia elétrica armazenada no capacitor é igual a da energia elétrica do sistema em .
Passo 1
Antes de começarmos a resolver o problema, vamos recordar de algumas coisas importantes desse tipo de circuito . A primeiro coisa é, como não há resistência, não há também perda de energia. Por isso, a carga elétrica e a corrente , e as respectivas energias armazenadas no capacitor e indutor, oscilam senoidalmente no tempo.
A energia armazenada no campo elétrico do capacitor varia com o tempo e é dada por
enquanto a energia armazenada no campo magnético armazenado no indutor também varia no tempo e tem a seguinte expressão
A carga armazenada nesse circuito é dada por
em que é a carga máxima armazenada no capacitor, é uma fase constante e a frequência de oscilação da carga é dada por
Para encontrarmos a corrente , basta derivarmos com relação ao tempo
Portanto, temos duas constantes que não conhecemos ainda: e . Para encontrar quais os valores delas, precisamos de duas condições iniciais. No caso, o problema deu para gente essas condições.
Para fechar, como , quando a gente substitui em e em e soma as duas para obter a energia total do circuito, obtemos o seguinte:
que não depende do tempo: a energia não é dissipada.
Passo 2
a) Depois dessa revisão, agora, sim, vamos resolver nosso problema...
Para , o problema deu duas condições iniciais para nós. A primeira delas é: o capacitor está totalmente carregado com carga , o que significa que
e a segunda é: a corrente é nula nesse instante de tempo, ou seja,
Resolvendo esta última equação, teremos e, substituindo isso em , vamos ter que . Com isso, as expressões ficam reescritas como
Para encontrarmos o tempo ’ em que a carga é da carga inicial , temos que fazer
O ângulo para o qual o cosseno tem esses valor é . Portanto, será dado por
Passo 3
c) No tempo , a energia do sistema é apenas a energia armazenada no capacitor, já que não há corrente no circuito: .
Para obtermos o tempo em que a energia do capacitor é igual a energia dele em , precisamos fazer a seguinte igualdade:
que vai nos dar que