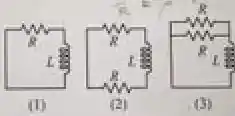
Ordene as constantes de tempo dos três circuitos abaixo, da maior para a menor. Considere todas as resistências e indutâncias com iguais valores respectivamente.
Passo 1
Bem... Sabemos da teoria que a constante de tempo de um circuito pode ser calculada por...
Onde é a resistência total do circuito. Então o que a gente tem que fazer é determinar a resistência total de cada circuito e comparar de cada um! Bora?
Passo 2
Para o circuito , a resistência total é a própria resistência já que ela é a única resistência...
Então...
Passo 3
Para o circuito , temos duas resistências em série. Consegue ver? É a resistência de baixo com a resistência de cima:

Então, de acordo com as nossas teorias de circuito, para resistências em séries, basta soma-las...
Então...
Passo 4
Para o circuito , temos duas resistências em paralelo...

Então, de acordo com as nossas teorias de circuito, para resistência em paralelo, basta usar a regra da soma e produto...
Logo...
Passo 5
Agora basta colocar em ordem de crescimento...
Resposta
Letra D.