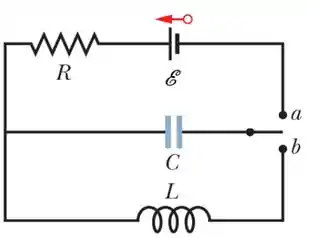
Na figura ao lado, , e e a fonte ideal tem uma força eletromotriz . A chave é mantida na posição durante um longo tempo antes de ser colocada na posição . Assinale abaixo a alternativa que indica a amplitude das oscilações da corrente, , no circuito após a chave ser colocada na posição .
(a)
(b)
(c)
(d)
(e)
Passo 1
Temos que antes da chave estar na posição passou-se um longo tempo com a chave na posição . Isso significa que passou tempo suficiente para que o capacitor fosse carregado no circuito !
Para descobrir a carga total no capacitor antes de ligar na chave basta fazer
Passo 2
Agora ligamos a chave na posição . Temos um circuito dessa vez! Pela lei das malhas nesse circuito temos
Como a corrente é dada por
A nossa equação diferencial fica
Cuja solução é dada por
Onde é a frequência de oscilação da carga e é a carga inicial no capacitor (que já calculamos).
Dessa forma a corrente vai ser dada por
A amplitude da corrente será
Outra forma de visualizar é lembrar que no circuito a energia é conservada e fica alternando entre o capacitor e o indutor (assim como em um oscilador harmônico a energia fica alternando entre potencial e cinética).
A energia máxima no capacitor é dada por
E a energia máxima no indutor é dada por
Igualando as duas
Que é a mesma relação que obtivemos antes!
Resposta
(c)