Para o circuito ilustrado na figura, o interruptor está aberto por um tempo muito longo
7a) Qual é a corrente no capacitor de no instante em que a chave é ligada?
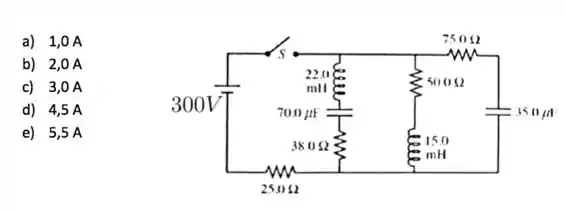
7b) Qual é a corrente no indutor de após a chave ter sido fechada por um tempo longo?
- 1,5 A
- 2,2 A
- 6,0 A
- 5,0 A
- 4,0 A
Passo 1
No caso da parte 7a) dessa questão, precisamos nos lembrar de que, no instante em que a chave é ligada, a corrente que passa pelos indutores é nula. Isso significa que, no trecho do circuito onde existem indutores, não haverá corrente elétrica e, portanto, nesse instante, só haverá corrente passando nos resistores de e da figura.
Assim, essa corrente passa por esses dois resistores que estão em série com resistência equivalente de . Isso nos permite encontrar o seguinte valor para a corrente nesta situação:
Passo 2
Já no caso da parte 7a) dessa questão, temos que analisar a corrente e seu valor para tempos muitos longos. Para tempos muito grandes, os capacitores atingem a carga máxima e, por essa razão, não há mais corrente atravessando o trecho do circuito que possui um desses capacitores completamente carregados.
No entanto, é importante notar que, para esses tempos muito longos que estamos analisando neste caso, há corrente que passa pelos indutores!! NÃO CONFUNDA ESTA SITUAÇÃO COM AQUELE DO ITEM ANTERIOR, EM QUE OLHAMOS PARA O TEMPO EM QUE A CHAVE S FOI LIGADA!!
Por isso, agora temos apenas os resistores de e o de e ambos estão em série: , o que nos dá a seguinte corrente elétrica
Resposta
Portanto, temos as seguintes respostas para esta questão:
7a) letra c).
7b) letra e).