O circuito LC oscilante representado na figura abaixo (despreze qualquer efeito dissipativo) é formado por um capacitor com capacitância e um indutor com indutância . Neste circuito, verifica-se que a tensão (diferença de potencial) máxima obtida é de .
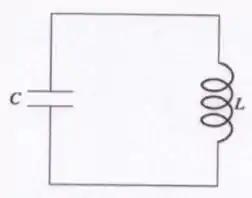
- Partindo do princípio de conservação da energia eletromagnética, obtenha a equação diferencial ordinária de segunda ordem que descreve a evolução temporal da carga no capacitor; a partir do resultado obtido em obtenha a frequência de oscilação (onde é a frequência angular do sistema) das cargas e da corrente neste circuito LC.
- Calcule o valor da carga máxima no capacitor e da corrente máxima no circuito.
- Calcule o valor da energia máxima armazenada no campo magnético do indutor.
Passo 1
a)
A energia total do sistema é a soma da energia do capacitor com a energia do indutor e deve ser constante, já que não há nenhum elemento dissipativo no circuito. Por isso
Se derivamos com relação ao tempo
Como , temos que . Substituindo isso na expressão acima, temos
Passo 2
A solução dessa equação diferencial é
em que é a carga máxima no circuito, é a frequência angular e é a fase, que depende das condições iniciais do problema.
Jogando essa expressão para na equação diferencial, teremos
Como essa igualdade deve ser zero para todo tempo, então,
Para completar, a corrente também oscilará no tempo e será igual a
sendo que o valor máximo da corrente será
Passo 3
b) A diferença de potencial do capacitor é dada por:
Dessa expressão, a gente vê que o potencial também oscila no tempo e tem valor máximo constante dado por
Passo 4
c) A energia armazenada no campo magnético do indutor é Substituindo a expressão para que encontramos no final do Passo 2, obteremos
que oscila no tempo.
Por isso, o valor máximo da energia armazenada no indutor é constante e tem o seguinte valor
Dos valores do enunciado, chegamos a