UFF – Física 2 – Provas Antigas – VS – 2022.1 – Questão 9
A figura mostra um gerador de corrente alternada ligado aos terminais de uma caixa preta. A caixa contém um circuito , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos. Medições realizadas do lado de fora da caixa revelam que:
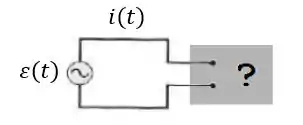
Com estas informações podemos afirmar que:
a) a corrente está adiantada em relação a e o circuito apresenta características indutivas ().
b) a corrente está adiantada em relação a e o circuito apresenta características capacitivas ().
c) a corrente está atrasada em relação a e o circuito apresenta características indutivas ().
d) a corrente está atrasada em relação a e o circuito apresenta características capacitivas ().
e) a corrente está em fase com a e o circuito apresenta características resistivas .
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que a gente diga qual é o comportamento desse circuito, quanto a impedância, dada uma de e uma corrente .
Mas e aí... como podemos definir esse comportamento??
Pra iniciar, vamos lembrar da Lei de Ohm (mas aqui utilizamos a impedância visto que trata-se de circuitos CA, certinho?):
Onde é a tensão alternada e é a corrente alternada.
Então bora lá para entender melhor tudo isso!!!
Passo 2
Bom... Podemos substituir pela dada na questão na fórmula do Passo 1, bem como a corrente também:
Para realizar essa divisão, vamos colocar e na forma polar:
Dessa forma, aplicando na fórmula, temos:
Beleza... descobrimos a impedância equivalente do circuito... mas o que podemos tirar disso?
Passo 3
Seguinte, sabemos que a impedância é a soma da resistência com as reatâncias capacitivas e indutivas de um circuito, né? Pois bem...
Analisando a resposta encontrada, temos que . Aquele que aparece ali indica o atrasado da tensão com relação a corrente, ou seja, a corrente está 42° atrasada com relação a corrente.
Dessa forma, para acontecer isso, é preciso que o circuito tenha característica capacitiva!!! Fazendo com que a reatância capacitiva do circuito seja maior que a reatância indutiva .
Entendeu direitinho? Responde aee ;)
Resposta
b) a corrente está adiantada em relação a e o circuito apresenta características capacitivas ().