Considere o circuito abaixo, onde é um capacitor de , um indutor de , e .
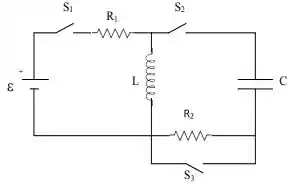
Fase 1: Chave fechada, com e abertas. O capacitor está totalmente descarregado. Determine:
a) A corrente no indutor após longo tempo com fechada e e abertas;
b) A energia transferida pela bateria ao indutor após longo tempo com fechada.
Fase 2: Depois de muito tempo, a chave é aberta e e são fechadas. Supondo quando e são fechadas, determine:
c) A expressão da corrente instantânea no indutor em função do tempo, a partir deste instante;
d) A diferença de potencial em a partir deste instante;
e) A soma das energias instantâneas armazenadas no capacitor e no indutor a partir deste instante. Justifique.
Fase 3: Se, após algum tempo, é aberta, permanecendo fechada e aberta, determine:
f) A carga no capacitor e a corrente no indutor um longo tempo após a abertura de ;
g) A energia dissipada no resistor um longo tempo após a abertura de . Justifique.
Passo 1
Ok! Então nesse primeiro tempo temos a chave sendo fechada e mantendo as demais abertas...
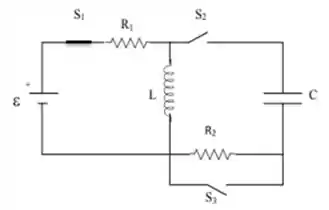
Nesse instante, repare que com as duas outras chaves abertas, não com o que se preocupar com essa parte da direita porque o circuito está aberto e não tem corrente indo para o outro lado. Então podemos simplificar para...
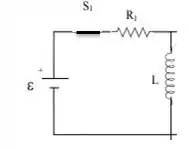
Passo 2
Bem, se a gente considerar muito tempo após o fechamento da chave , e levando em conta de que é um sistema de corrente contínua, o indutor se transforma em apenas um curto circuito e que conduz uma corrente contínua :
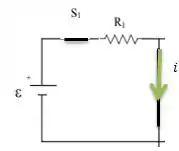
E essa corrente pode ser determinada pela Lei de Ohm...
Passo 3
A energia transferida para o indutor é a energia armazenada no campo magnético desse indutor dado pela teoria por...
Como o indutor tem uma indutância de (ou ) e a corrente ...
Passo 4
Nesse instante então () a chave é aberta, e são fechadas...
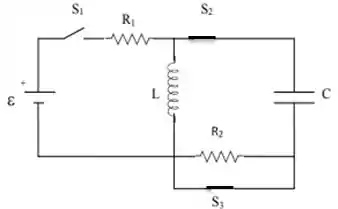
Repare que aí já não vai mais fazer sentido continuar representando o circuito com a fonte, pois agora ele é quem é o circuito aberto (que não circula corrente)...
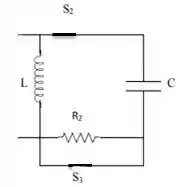
E ainda, olha que maravilha, temos um curto circuito ali no resistor , pois entre o caminho de resistência (a chave) e o de resistência, ela passa pelo caminho de resistência . Ou seja, para efeito de análise de circuito, também podemos desconsiderar...
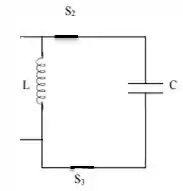
PRONTINHO! Resumindo, quando essa fase se inicia, temos então um circuito . Agora partiu responder as perguntas?
Passo 5
Na Letra C temos que determinar a corrente em todo instante de tempo .
Bem, de acordo com a teoria sobre circuito , a corrente que circula em um circuito será senoidal de valor...
Onde é a corrente inicial no indutor e é a frequência angular de oscilação do circuito.
Bem, para a corrente , como sabemos que no indutor não pode haver variação brusca de corrente, a corrente imediatamente após as chaves se fecharem e abrir, a corrente que passa no indutor é , lá do passo 2. Então ela deve permanecer a mesma nesse primeiro instante ...
Logo...
Já o pode ser dado por...
Então...
Ou seja...
SIM! É uma frequência muito alta! Isso significa que a corrente oscila muito rápido...
Passo 6
Ora! Nós vimos ali no passo 4 que o resistor após se fechar vira um curto-circuito, o que significa que a diferença de potencial em cima dele é...
Passo 7
Bem, nesse instante , a energia do circuito é a energia armazenada no indutor () somado com a energia armazenada no capacitor ()...
Como não tem nenhum resistor nesse instante (circuito sem amortecimento ) a energia se conserva em todo instante de tempo (desde o tempo ).
No tempo , a energia do indutor foi calculada...
Só que o problema nos disse que inicialmente a energia do capacitor era de , já que estava descarregado inicialmente! Então...
Essa é então a energia total do circuito .
Passo 8
Nessa fase 3 a chave é então reaberta...
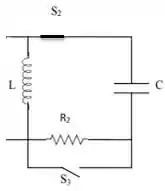
Nesse instante de tempo, passa a circular uma corrente no resistor que estávamos ignorando até o momento, então ele volta a aparecer no circuito formando um circuito amortecido .
Passo 9
Na letra D é a para agente considerar o circuito muito tempo assim e determinar a carga no capacitor () e a corrente no indutor ().
Ora! A presença de um resistor na parada faz o sistema se descarregar, de modo que após um longo período de tempo, a carga no capacitor se torna nula e a corrente para de circular...
Passo 10
Bem! Como o resistor é um elemento dissipativo de energia, ele vai dissipar em forma de calor toda energia do sistema calculada no passo 7 fazendo o circuito perder toda sua energia e então parar de circular a corrente como já vimos no passo anterior. Então...
Resposta
Letra A:
Letra B:
Letra C:
Letra D:
Letra E:
Letra F:
Letra G: