UFF - Física 3 - P3 2017.1 - 4
Em um circuito , tem-se uma bobina de indutância e uma resistência de Se o circuito está conectado em série a uma fonte de força eletromotriz de , qual será a energia armazenada no campo magnético após a corrente atingir o seu valor máximo?
Passo 1
O problema é a respeito de um circuito RL, que representamos abaixo.
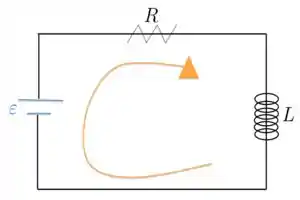
A seta em amarelo nessa figura é o sentido que a gente escolheu para aplicar na lei das Malhas de Kirchoff, ok? Bom, aplicando essa lei, chegamos a:
Ok até aqui? Só aplicamos a lei das Malhas até agora…
Passo 2
O detalhe dessa questão é que você não precisa resolver a equação diferencial acima \0/ !! Olha lá no enunciado e veja que se pergunta sobre a energia do campo para a corrente máxima !! Nesse momento que a corrente é máxima (quando é muito grande: ), o que acontece com a taxa de variação da corrente como tempo? É ZERO, PORQUE A CORRENTE ATINGIU O SEU VALOR MÁXIMO. Pronto, você acabou de matar a questão!! Duvida?? Dá uma olhada na sequência:
sendo que . Com os dados do problema, .
Resposta
A energia armazenada no campo magnético do indutor é
que é a resposta da letra e).