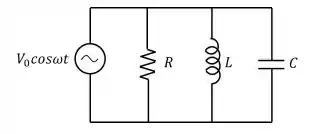
Uma fonte aplica ao circuito abaixo uma diferença de potencial . Considere ainda a impedância do circuito. A corrente que passa através do indutor será:
a)
b)
c)
d)
e)
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão queremos o valor da corrente que passa pelo indutor.
Aí eu te pergunto: Como podemos verificar isso com análise de circuitos?

Passo 2
Bom... primeiramente vê-se que a tensão está aplicada igualmente em cada componente do circuito, portanto temos para a corrente no indutor:
Em que é a impedância indutiva.
Passo 3
Dessa forma, substituindo os valores de e em suas formas complexas, obtemos (utilizando apenas a parte real do número complexo):
Entendeu direitinho? Responde aee ;)

Resposta
d)