Considere o circuito abaixo com cargas e nas placas do capacitor. A chave é fechada no instante .
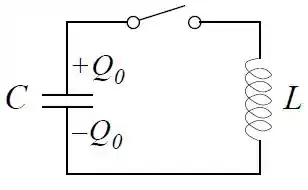
- Escreva a equação diferencia da carga na placa superior do capacitor. Explicite a condição inicial para .
- Determine a carga na placa superior e a corrente no circuito para e que satisfazem as condições iniciais.
- O indutor é formado por um solenoide muito longo de comprimento e diâmetro com voltas de fio uniformemente enroladas em um núcleo de plástico (a permeabilidade do plástico é igual à do vácuo). Calcule a indutância.
- Qual é a nova frequência angular de oscilação se o núcleo de plástico for substituído por um núcleo de ferro com permeabilidade magnética ? Expresse sua resposta em termos da frequência angular do circuito com o solenoide com núcleo de plástico.
Passo 1
- Escreva a equação diferencia da carga na placa superior do capacitor. Explicite a condição inicial para .
- Determine a carga na placa superior e a corrente no circuito para e que satisfazem as condições iniciais.
- O indutor é formado por um solenoide muito longo de comprimento e diâmetro com voltas de fio uniformemente enroladas em um núcleo de plástico (a permeabilidade do plástico é igual à do vácuo). Calcule a indutância.
- Qual é a nova frequência angular de oscilação se o núcleo de plástico for substituído por um núcleo de ferro com permeabilidade magnética ? Expresse sua resposta em termos da frequência angular do circuito com o solenoide com núcleo de plástico.
Bom, sabemos que a soma de todas as ddps de um circuito deve ser nula, certo? Logo:
Mas sabemos que ... substituindo isso aqui em cima:
Essa é uma equação diferencial de segunda ordem e podemos escrevê-la como:
A condição inicial é que inicialmente, a carga na placa superior do capacitor seja máxima.
Passo 2
Beleza! Conforme eu falei, a equação:
É uma equação diferencial de segunda ordem e a cara dela é bem familiar... ela tem a mesma cara da equação para um sistema massa-mola sem amortecimento.
A solução dessa equação diferencial vai ser algo do tipo:
Sabemos que em , . Logo:
Além disso, sabemos que em , .
Portanto, a solução da equação diferencial é:
Passo 3
A indutância é dada por:
Então temos que começar nos preocupando com o fluxo do campo magnético.
O campo magnético de um solenoide é dado por:
O fluxo do campo magnético para um solenoide com espiras é dado por:
Agora podemos finalmente calcular a indutância:
Passo 4
A frequência angular é dada por:
A nova indutância será dado por:
Nesse caso, . Substituindo na fórmula da indutância:
Assim, a nova frequência será:
Lembrando que:
Por fim: