No circuito abaixo, um capacitor completamente carregado com capacitância igual a é conectado a um indutor de . O que acontece após a chave ser fechada?
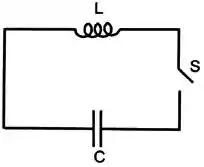
- A carga do capacitor se anula instantaneamente.
- A carga do capacitor decresce exponencialmente a zero.
- A carga permanece inalterada.
- A carga oscila com um período de .
- A carga oscila com um período de .
Passo 1
Para você ficar fera nesse tipo de questão de circuito LC, dá uma olhada na P3 da UFF 2017.1, questão 6 resolvida que a gente tem aqui no Responde Aí. Lá nessa questão, discutida passo a passo, você vai ver uma discussão breve, mas suficiente, de como é a analogia desse tipo de circuito elétrico com o MHS de uma partícula massiva... ;-)
Você vai ver lá que a carga, e portanto a corrente do circuito, oscila no tempo com uma frequência angular característica dada por
Substituindo os valores fornecidos no enunciado, obtemos que o period de oscilação da carga é
Portanto, a carga no circuito oscila com um período de .
Resposta
Portanto, o item correto é o da letra d).