Física 2 - UFF; P3 de 2019.1
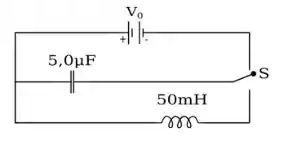
6 - No circuito mostrado abaixo, o interruptor S é primeiro empurrado para cima para carregar o capacitor. Quando S é então empurrado para baixo, a corrente no circuito irá
- oscilar a uma frequência de .
- oscilar a uma frequência de .
- oscilar a uma frequência de .
- diminuir exponencialmente com um tempo característico de .
- diminuir exponencialmente com um tempo característico proporcional a .
Passo 1
Ora, estamos falando de um circuito (indutor e capacitor associados). Você deve se lembrar de que esses elementos não liberam energia na forma de calor (o cara que faz isso é o resistor). Se isso não acontece, a energia fica “presa” no circuito passando de um lado para outro (oscilando).
Isso já cancela D e E.
Passo 2
Para descobrir a frequência de ressonância , devemos usar a frequência angular de ressonância de um circuito LC, no qual basta fazer:
Mas está relacionada com a frequência por...
Então...
Se lembrando de que e ...
Resposta
Letra B.
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.