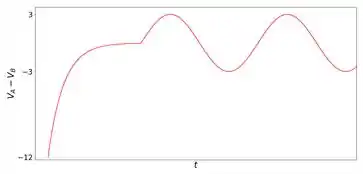
A figura mostra um circuito utilizado para a geração de picos de alta tensão. Neste circuito acorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberta durante longo tempo
Fase 2: chave aberta e fechada durante longo tempo
A figura mostra o gráfico da d.d.p. durante as fases e
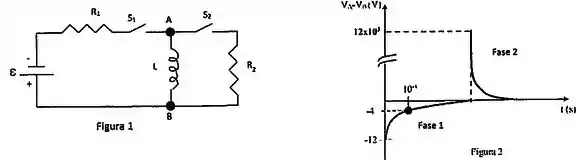
Com o indutor inicialmente sem corrente, determine:
- A expressão para a d.d.p. em função do tempo na fase a partir do instante de tempo no qual o interruptor é fechado. Deixe a expressão em função de , e .
- Os valores de , e sendo e assumindo (base dos logaritmos neperianos). Sugestão: utilize informações contidas no gráfico da figura considerando as fases e
- Trace o gráfico da d.d.p. em função do tempo nas fases e . Em outras palavras desenhe a nova figura para este circuito.
Supondo agora que o resistor seja retirado e no seu lugar seja colocado um capacitor . Além disso, os valores de , e são os mesmos encontrados nos itens anteriores. Com este novo circuito as fases e 2 são repetidas.
Passo 1
Na fase temos um circuito onde a corrente no instante inicial no indutor é nula. Nessa malha temos
Cuja solução para a corrente é dada por
Com .
E a diferença de potencial é a diferença de potencial no indutor
A d.d.p. no indutor é dada por
Assim
Passo 2
Na fase temos pelo gráfico dois valores de
O primeiro valor do gráfico é
Substituindo na fórmula que achamos no item anterior
Passo 3
O segundo valor no gráfico é dado por
Substituindo na fórmula que achamos no item anterior (e já usando o valor )
Tirando o log dos dois lados na base
O enunciado pede para considerar
Como
Passo 4
No começo da fase temos no indutor a corrente máxima e um circuito com somente um solenóide e a resistência .
No final da fase a corrente é dada por
E essa será a corrente no início da fase .
No início da fase a voltagem sobre o solenóide (e consequentemente sobre a resistência ) é, de acordo com o gráfico . Assim
Passo 5
Na fase 1 sabemos que a voltagem é negativa e tende a exponencialmente.
Agora na fase 2 trocamos essa resistência por um capacitor de capacitância .
Pela lei das malhas temos
Lembrando que
Cuja solução é
Onde .
Derivando em relação ao tempo achamos a corrente
Assim a d.d.p (que é a d.d.p. do solenóide) é dada por
Ou seja, na segunda fase a d.d.p será uma função tipo seno com amplitude
Assim o esboço dessa voltagem é algo tipo
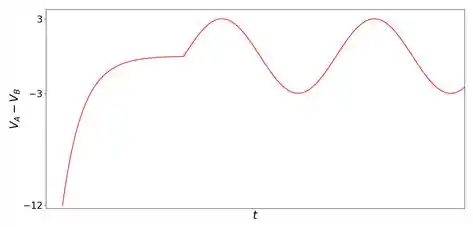
Resposta
(a)
(b), e
(c)