(Esta questão compõe-se de 3 itens independentes.)
Uma bateria de constante é conectada a um indutor num circuito de malha simples. A resistência equivalente do circuito vale . No instante em que a bateria é ligada no indutor, a corrente é nula. Sabendo que a corrente que atravessa o circuito é dada pela função , calcule o valor da indutância .
Um capacitor inicialmente carregado com , é conectado a um indutor pelo qual inicialmente não passa corrente. A resistência equivalente deste circuito de malha simples vale . Encontre a expressão da carga no capacitor em função do tempo, .
O circuito oscilante da figura possui resistência desprezível. O capacitor vale e, em , possui carga . O indutor, também em , possui energia e está sendo atravessado pela corrente com o sentido mostrado na figura. Calcule a carga máxima no capacitor.
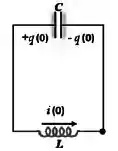
(SUGESTÃO: Lembre-se da conservação de energia). Use
Passo 1
Uma bateria de constante é conectada a um indutor num circuito de malha simples. A resistência equivalente do circuito vale . No instante em que a bateria é ligada no indutor, a corrente é nula. Sabendo que a corrente que atravessa o circuito é dada pela função , calcule o valor da indutância .
Em um circuito , a corrente varia com o tempo de acordo com a função:
Sabendo isso, o nosso trabalho aqui é comparar a função acima com a função dada pelo problema:
Daqui podemos tirar que:
Além disso:
Passo 2
Um capacitor inicialmente carregado com , é conectado a um indutor pelo qual inicialmente não passa corrente. A resistência equivalente deste circuito de malha simples vale . Encontre a expressão da carga no capacitor em função do tempo, .
Em um circuito , a carga varia com o tempo de acordo com a função:
Onde , lembrando que .
Então, logo de cara, já podemos calcular algumas coisas?
Substituindo esses caras na expressão de , teremos:
Para descobrir os valores de e , teremos que usar as condições iniciais do problema.
Passo 3
De acordo com o enunciado, e . Então vamos utilizar essas informações pra descobrir os valores de e , ok?
Além disso:
Utilizando a igualdade trigonométrica , teremos:
Elevando os dois lados ao quadrado:
Finalmente:
Voltando para a primeira condição de contorno, teremos:
Substituindo e na expressão de , teremos:
Passo 4
O circuito oscilante da figura possui resistência desprezível. O capacitor vale e, em , possui carga . O indutor, também em , possui energia e está sendo atravessado pela corrente com o sentido mostrado na figura. Calcule a carga máxima no capacitor.
A energia total do circuito será a soma das energias do indutor e do capacitor, logo:
Onde .
O capacitor terá carga máxima quando toda a energia do circuito estiver armazenada nele, logo:
Finalmente:
Resposta