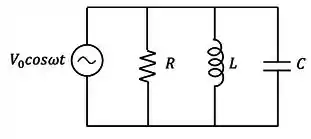
a)
b)
c)
d)
e)
Passo 1
Como o indutor possui inércia de corrente, isso significa que essa corrente chega atrasada. Atrasos de corrente significa que o desvio de fase é negativo (afinal, atrasar é uma coisa negativa!).
O atraso negativo tem magnitude de . Por tanto, seja lá o que for, nós temos:
Com isso a gente fica entre a (c) e a (d).
Passo 2
Esse “alguma coisa” é a corrente máxima, que é igual à tensão máxima () dividida pela impedância do indutor, que vale . Dividindo:
Resposta
Letra (d).
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.