Considere o circuito abaixo, onde e . A corrente elétrica gerada pela fonte de força eletromotriz , após o circuito ficar ligado por um tempo muito maior que a constante de tempo indutiva é:
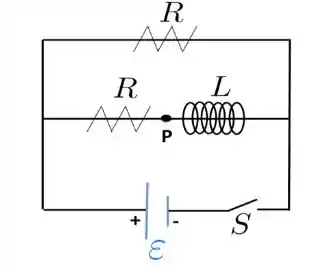
a)
b)
c)
d)
e)
Passo 1
Essa questão é interessante e espero que te convença disso e, mais que isso, quero te ajudar a entendê-la para que depois você tenha confiança para mandar bem em outras parecidas. Bora lá?
A primeira coisa tentadora, e correta, que vem na nossa cabeça em uma questão dessas é aplicar a lei das malhas e dos nós no circuito, né? Isso também te levaria à solução! Mas tem um grande pulo do gato nessa questão e o segredo está na expressão: “tempo muito maior que constante de tempo indutiva”. Vamos ver…
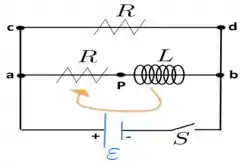
Para isso, considere somente a malha em amarelo na figura abaixo. Isso vai nos dar o seguinte:
Passo 2
Agora, foca no “tempo é muito maior do que a constante de tempo indutiva”, pois nesse caso a corrente que passa no seguimento ab do circuito acima já atingiu o seu valor máximo ! Em termos de matemática, a gente sabe, então, que a variação da corrente é nula .
Significa que diferença de potencial entre as extremidades do indutor é nula! Ou seja, passa corrente no segmento ab, mas diferença de potencial no indutor é ZERO. Assim, a gente pode esquecer o indutor (nesse tempo muito maior do que a constante indutiva!!) e remontar nosso circuito da seguinte forma:
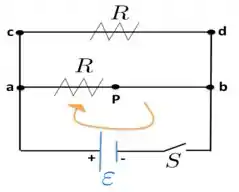
Confessa, agora você está muito mais “em casa” do que antes, né? Dois resistores em paralelo com ambos os segmentos ab e cd submetidos à mesma diferença de potencial ! Só calcular a resistência equivalente e partir pro abraço…rsrs
Passo 3
Colocando em contas, essa conversa toda de antes mostra que a resistência equivalente do circuito acima é:
E a corrente fica:
Essa é a corrente elétrica gerada pela força eletromotriz pedida pelo problema! Seguiu bem a ideia? Fique sempre atento a situações como essa em que existe “tempos muito maiores do que...” ;-)
Resposta
Letra b).