Unicamp - Física 3 – P3 2018.1 - NOTURNO - 8
Uma fonte de fem alternada, com uma certa amplitude e frequência , é ligada separadamente a um resistor, a um capacitor e a um indutor. Depois que a fonte é ligada, faz-se variar e mede-se a amplitude da corrente resultante. A variação de com é mostrada no gráfico abaixo. A correspondência exata entre as curvas da figura e os dispositivos é:
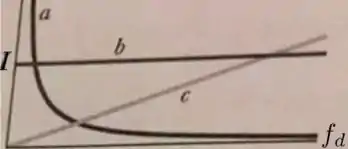
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
Passo 1
Vamos considerar que a fonte de corrente alternada tem uma diferença de potencial dada por
em que é a frequência de oscilação da fonte, é o maior valor (amplitude) que a tensão pode ter e é uma fase que depende das condições iniciais do problema.
Vamos começar a analisar o caso do resistor. Quando ele está ligado à fonte, podemos usar a lei das malhas para escrever
Se a gente olha para essa expressão, vemos a corrente no resistor oscila no tempo e tem valor máximo dado por
que não depende da frequência .
Por isso, a curva representa o resistor.
Passo 2
Agora, no caso do capacitor, a lei das malhas dá como resultado os seguinte:
Como a corrente é ,
Dessa expressão, vemos que a corrente também oscila no tempo e tem valor máximo dado por
que aumenta linearmente com a frequência da fonte.
Por isso, a curva da figura representa o capacitor.
Passo 3
Aplicando a lei das malhas par ao indutor, temos
Se integramos essa expressão, acharemos uma corrente dada por
Nesse caso, o valor máximo da corrente (sua amplitude!) é igual a
e diminui à medida que a frequência aumenta.
Por isso, a curva da figura representa o indutor.
Resposta
Letra c.