No circuito da figura abaixo, considere as seguintes fases:
Fase 1: e fechadas e aberta por um longo tempo.
Determine a corrente no indutor no início e no final da Fase 1.
Calcule a energia final armazenada no indutor .
Fase 2: e abertas e fechada durante logo tempo.
Fase 3: e abertas e é fechada.
Determine a frequência angular da fonte para que a corrente na malha tenha a maior amplitude possível.
Se , faça o diagrama dos fasores da malha e calcule o ângulo de fase entre e .
Determine a potência média fornecida pela fonte e a potência média dissipada em .
Dados: , , , , e
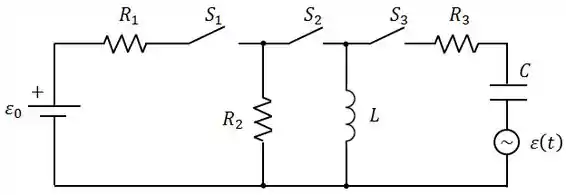
Passo 1
Determine a corrente no indutor no início e no final da Fase 1.
Com e fechadas, o circuito é formado por , , e .
Nesse circuito, a corrente através do indutor será dada por:
Em , assim que as chaves são fechadas, a corrente no indutor é nula (toda a corrente vai para ), logo:
No final da Fase 1, ou seja, quando , toda a corrente circuito passa através do indutor (não haverá corrente passando por ), logo:
Onde e . Logo:
Passo 2
Calcule a energia final armazenada no indutor .
A energia no indutor é dada por:
Como já vimos na letra , no final da Fase 1, a corrente no indutor é dada por:
Logo, sabendo que :
Passo 3
Determine a frequência angular da fonte para que a corrente na malha tenha a maior amplitude possível.
Obs.: Durante a Fase 2, em que e são abertas e é fechada por um longo tempo, o circuito será formado somente por e , onde a energia que estava acumulada no indutor no final da Fase 1 será totalmente dissipada no resistor .
Na Fase 3, o circuito será formado por , , e , logo, é um circuito .
Para que a corrente na malha tenha a maior amplitude possível, é necessário que a frequência seja a frequência de ressonância, definida por:
Onde:
Logo:
Passo 4
Se , faça o diagrama dos fasores da malha e calcule o ângulo de fase entre e .
Para fazer o diagrama de fasores e calcular o ângulo de fase, primeiro precisamos calcular as reatâncias capacitiva e indutiva, dadas por:
As tensões são dadas por:
Logo, o diagrama de fasores vai ter essa cara:
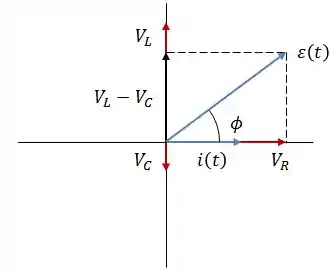
Passo 5
O ângulo de fase é dado por:
Passo 6
Determine a potência média fornecida pela fonte e a potência média dissipada em .
A potência média fornecida, por definição, é dada por:
Ok, as únicas coisas que estão faltando aqui são a corrente máxima e . Pra calcularmos esse cara, vamos usar a equação:
Onde é a impedância.
Substituindo os valores, teremos:
Passo 7
Podemos calcular o através da , que nós já calculamos:
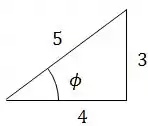
Logo:
Passo 8
Agora podemos calcular a potência média fornecida.
Passo 9
A potência média dissipada no resistor é dada por:
Onde .
A potência média dissipada em é igual à potência média fornecida pela fonte, o que faz bastante sentido porque o resistor é o único elemento desse circuito que dissipa energia. Logo, toda a energia do circuito vai ser dissipada pelo resistor.
Resposta