UFJF – Física 3 – AV3 – 2018/1
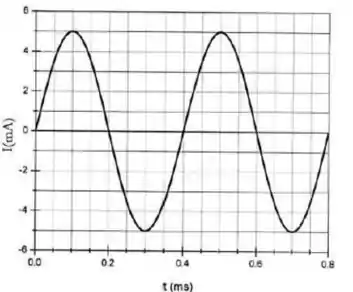
3) Um capacitor é carregado por uma bateria de 12V. Em seguida, no instante , é ligado a um indutor. O gráfico mostra o comportamento da corrente no circuito em função do tempo . A partir do gráfico, determine:
a) A frequência de oscilação da corrente.
b) Os valores da capacitância e da indutância .
c) A carga máxima do capacitor.
d) As expressões para as energias armazenada no capacitor e , no indutor.
e) Faça um gráfico das tensões no indutor e no capacitor em função do tempo para o intervalo de tempo . Pode ser apenas um esboço, mas use o gráfico ao lado como um guia de formato.
f dz
Passo 1
Falaaa... belezinha???
Nessa questão vamos calcular, na letra a, a frequência de oscilação da corrente lembrando que a frequência é o inverso do período. (vamos usar o gráfico)
Na letra b, vamos usar que:
E a relação:
E na letra c:
Passo 2
Letra a)
Para achar o período, pegamos dois picos da função e subtraímos o tempo um do outro:
E aí achamos a frequência:
Passo 3
Na letra b)
Pra achar a indutância vamos usar:
Vamos pegar um pedaço, no começo do gráfico, que tenha o formato beeem próximo de uma reta, daí podemos fazer a aproximação:
Como temos:
E para calcular a capacitância:
Resposta
a)
b) e