Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RLC

Ver Teoria
Exercício 191234567891011121314151617182021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687

Enunciado

Circuitos CA

No circuito da figura a chave a é fechada num determinado instante:

  1. Qual será a corrente inicial? Justifique.
  2. Qual será a diferença de potencial sobre o indutor 1   m s após a chave a ser fechada?

    3. 1 segundo depois da chave a ser fechada, ela é aberta e simultaneamente a chave b é fechada:

  3. Qual a carga máxima que o capacitor poderá atingir?
  4. Quanto tempo leva para o capacitor atingir a carga máxima?

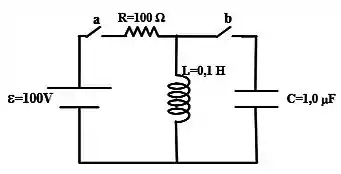
Passo 1

Como temos um indutor, a corrente não sofre variação instantânea, logo seu valor inicial é zero.

Passo 2

Pela fórmula temos que

i t = E R 1 - e - R t L = 1 - e - 1000 t

Então, para calcularmos a ddp no indutor, usamos a fórmula

V L = L d i d t = 0,1 1000 e - 1000 t

Pata t = 1   m s

V L = 100 e - 1 = 37   V

Passo 3

Passado 1   s , a corrente já está estabilizada e a corrente que passa sobre o indutor é

i = E R = 100 100 = 1   A

Como não há variação instantânea de corrente, ela permanece valendo 1   A .

Sabemos que esta é a corrente máxima e que pode ser calculada, também, pela fórmula do capacitor:

i m á x = Q m á x ω

Logo,

Q m á x = 1 ω

E

ω = 1 L C = 1 0,1 ∙ 1 ∙ 10 - 6 = 10 ∙ 10 3 r a d s

Então,

Q m á x = 10 ∙ 10 - 4   C

Passo 4

A carga máxima é atingida em t = T / 4 . Fica mais fácil de ver com o desenho abaixo, onde o pico representa o momento que o capacitor atinge a caraga máxima.

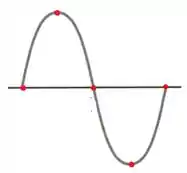
Agora é só fazer o cálculo do período.

T = 2 π ω

T = 2 π 10 ∙ 10 3 = 2 π 10 ∙ 10 - 4   s

Então,

t = π 2 10 ∙ 10 - 4   s

Resposta

  1. i t = 0 = 0
  2. V L = 37   V
  3. Q m á x = 10 ∙ 10 - 4   C
  4. t = π 2 10 ∙ 10 - 4   s

Exercícios de Livros Relacionados

Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.