Circuitos CA
Um circuito é composto por um capacitor de e um indutor de . Em o capacitor está totalmente descarregado e a corrente vale . Calcule:
- Calcular a corrente máxima no circuito.
- A carga máxima no capacitor.
- O instante em que a energia armazenada no capacitor alcança o valor máximo pela primeira vez.
Passo 1
Essa é simples. O enunciado diz que o capacitor está totalmente descarregado, isto é, o circuito já se encontra na condição de corrente máxima. Logo,
Passo 2
Sabemos como calcular a corrente máxima:
E sabemos calcular que em um circuito :
Então,
Passo 3
Bem, sabemos que o período de oscilação da carga no capacitor é calculado por . A energia é máxima quando a carga é máxima, logo, será em .
O desenho abaixo facilita a entender este tempo igual a do período. A primeira bolinha é , a segunda bolinha é , a terceira bolinha é , a quarta bolinha é e última bolinha é .
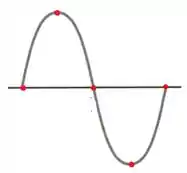
Fazendo os cálculos:
E
Resposta
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.