Considere as seguintes afirmações sobre um circuito LC ideal:

I - A diferença de potencial elétrico no indutor é máxima quando a corrente elétrica que o atravessa é máxima.

II - A energia armazenada no capacitor é nula quando a corrente elétrica que o atravessa é máxima.

III - A energia armazenada no indutor é nula quando a corrente elétrica que o atravessa é nula.

São CORRETAS as afirmações:

1. I e II
2. II e III
3. I e III
4. I, II e III
5. II, apenas.

Cara, antes de a gente analisar esses três itens vamos relembrar algumas coisinhas da teoria sobre circuito LC (indutor junto com um capacitor )...

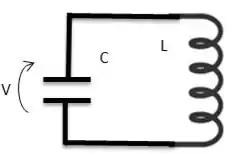
Vamos supor que inicialmente o capacitor encontra-se carregado com um potencial V. Assim que o indutor é conectado, uma corrente surge no circuito, através da qual a energia acumulada no capacitor, por meio do campo elétrico, passa a se transferir para o indutor, que armazena energia pelo campo magnético.

Bem... Como o campo magnético no indutor precisa de corrente, podemos falar que a energia no indutor será máxima quando a corrente nele for à máxima corrente:

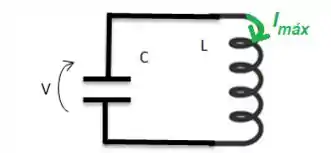
Nesse mesmo momento em que a corrente é máxima no circuito e a energia é máxima no indutor, temos uma energia nula no capacitor, já que toda a carga elétrica está na corrente e não na chapa do capacitor.

Contudo, entretanto, não obstante... Quando a corrente é nula, então podemos dizer que toda a carga vai estar concentrada no capacitor:

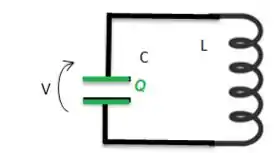
Vai ser quando a energia no capacitor vai ser máxima, devido a carga concentrada na chapa do capacitor, ao passo que devido a falta de corrente, a energia no indutor será nula!

PERFEITO! Com essa revisão da teoria, podemos revisar agora os itens! Vamos nessa?