Passo 1
Como cada um tem uma velocidade em um eixo, podemos decompor a velocidade pra acharmos a relação entre as velocidades de cada um de acordo com a figura (OBS.: repare bem como orientamos os eixos x e y, hein 
)
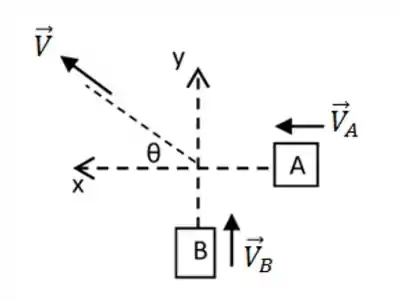
Passo 2
Vamos usar aqui o nosso princípio de conservação do momento linear!
Dessa relação, encontramos que o vetor velocidade final com que o sistema se move é dado por:
Esse mesmo vetor pode ser escrito como:
De onde tiramos as seguintes relações:
Usando :
Porém ele quer o inverso dessa razão
Resposta
Exercícios de Livros Relacionados
Dois veículos espaciais em órbita estão acoplados. A massa de um deles é de 1000 Kg e a do outro de 2000 Kg. Para separá-los, é denotada entre os dois uma pequena carga explosiva, que comunica uma ene
Vários pesquisadores em ensino de física alegam que parte da origem das concepções alternativas entre os estudantes são os efeitos especiais que eles veem em desenhos animados e em filmes. Usando a co
Uma espaçonave é separada em duas partes pela detonação dos rebites explosivos que as mantêm unidas. As massas das partes são 1200k g e 1800k g ; o módulo do impulso que a explosão dos rebites exerce
"Relativamente" é uma palavra importante. Na Fig. 9-72, o bloco E de massa m e =1,00k g e o bloco D de massa m D=0,500k g são mantidos no lugar com uma mola comprimida entre os dois blocos . Quando os
Um certo núcleo radioativo (pai) se transforma em um núcleo diferente (filho) emitindo um elétron e um neutrino. O núcleo pai estava em repouso na origem de um sistema de coordenadas x y . O elétron s