UFRJ, Sem Campus, Física 1, Roteiros de F1 - UFRJ - Roteiro 10 - Colisões, Questão 9
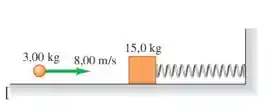
Um bloco de 15,0 kg é preso a uma mola horizontal muito leve com constante de força 500,0 N/m e está apoiado sobre uma mesa horizontal sem atrito (Figura). De repente, o bloco é atingido por uma pedra de 3,00 kg seguindo na horizontal a 8,00 m/s para a direita, quando a pedra recua a 2,00 m/s horizontalmente para a esquerda. Determine a distância máxima que o bloco comprimirá a mola após a colisão.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um bloco que está preso a uma mola horizontal. O bloco é atingido por uma pedra.
A questão nos pede para calcularmos a distância máxima que o bloco comprimirá a mola após a colisão.
Para isso, devemos utilizar o princípio da conservação do momento linear:
“O momento linear total de um sistema isolado permanece constante se nenhuma força externa atuar sobre ele.”
Em outras palavras, o momento antes da colisão é igual ao momento depois da colisão , ou seja:
Em seguida, aplicaremos o principio da conservação de energia mecânica:
“quando nenhuma força dissipativa atua sobre um corpo, toda a sua energia relativa ao movimento é mantida constante”
Em outras palavras:
E aí? Bora lá?
😉
Passo 2
Dessa forma, pela conservação do momento linear, temos:
Onde:
- e são as massas da pedra e do bloco, respectivamente;
- e são as velocidades iniciais da pedra e do bloco, respectivamente;
- e são as velocidades finais da pedra e do bloco, respectivamente.
Assim, substituindo os valores, temos:
Passo 3
Agora que temos a velocidade final do bloco, podemos descobrir a compressão total da mola.
Pela conservação de energia, temos que a energia cinética do bloco será igual a energia potencial elástica da mola, ou seja:
Onde é a constante elástica.
Logo, substituindo os valores, temos que a compressão total da mola é dada por:
Entendeu direitinho? Responde aee ;)
