Dois carros idênticos colidem em três experimentos em um trilho sem atrito. Em cada caso, o carro A está inicialmente com velocidade e o carro está em repouso. Esquematize o gráfico velocidade tempo para cada carro
- Se os carros ficam grudados após a colisão
- Se o carro A é estacionário depois da colisão, e
- Se o carro A tem velocidade depois da colisão
- Interprete as colisões em cada caso.
Passo 1
Estamos lidando com um problema de conservação de momento. Quando lidamos com esse tipo de problema, precisamos nos atentar que tudo ocorre em dois momentos distintos, um ANTES e um DEPOIS, e que a conservação ocorre pois todo o momento antes é igual ao momento depois da colisão.
Sabemos que o momento é descrito por , podemos a partir das informações apresentadas no enunciado, que
Passo 2
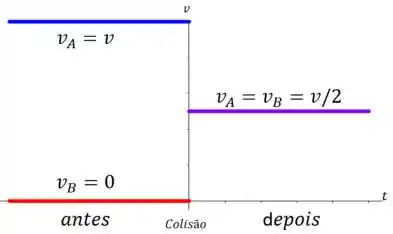
(a) Se os carros ficam grudados após a colisão ... temos que o momento depois é dito por
Na qual é a massa total dos dois carros que estão grudados, ou seja,
Com o enunciado nos dá que os carros são idênticos, mesmo que eu não saiba quem é , eu sei que , então usando a conservação de momento, temos que
Ou seja, a velocidade depois da colisão dos dois carros grudados é a metade da velocidade inicial do carro e o sentido ainda é o mesmo.
Passo 3
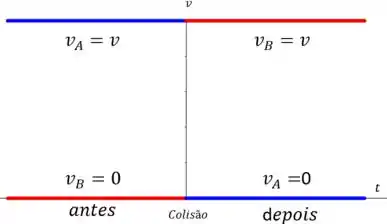
(b) Se o carro A é estacionário depois da colisão ... teríamos que a velocidade do carro seria nula depois da colisão. Então o momento depois da colisão será
Na qual aqui é a velocidade do carro depois da colisão. Então usando a conservação de momento, temos que
Ou seja, o carro passa a ter a mesma velocidade e o mesmo sentido que o momento possuía antes.
Passo 4
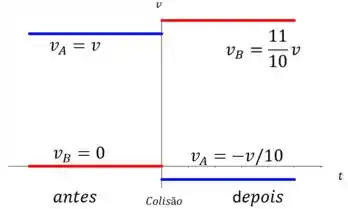
(c) se o carro tem velocidade depois da colisão ... então o que temos é que o sentido do carro alterou depois da colisão. O momento depois é descrito por
Na qual é a velocidade do carro depois da colisão. Assim temos que pela conservação de momento
Cortando a massa de todos os termos e passando os termos para o outro lado, temos
Passo 5
(d) Interprete as colisões em cada caso ...
Existem formas de analisar os tipos de colisões. Uma das formas é utilizando a energia cinética do sistema formado pelos dois carrinhos (A e B) antes e depois da colisão. A energia cinética do sistema é igual à energia cinética do carrinho A mais a energia cinética do carrinho B . Logo, as energias cinéticas do sistema antes e depois da colisão será:
Se , temos uma colisão perfeitamente elástica.
Se e , temos uma colisão inelástica.
Se e , temos uma colisão perfeitamente inelástica, porque nesse caso a diminuição da energia cinética do sistema será máxima!
Por fim, se , o sistema formado pelos carros A e B ganhou energia através de trabalho.
Para os três casos:
e
Para o primeiro caso
Logo, a energia cinética será:
Por isso:
Então, a primeira colisão é dita perfeitamente inelástica.
Para o segundo caso
e
e
Logo, a energia cinética será:
Por isso:
Desta forma, a segunda colisão é dita perfeitamente elástica.
E o terceiro caso
e
Logo, a energia cinética será:
Por isso:
Logo, o sistema formado pelos carros A e B ganhou energia através de trabalho.
Resposta
- e
- e
- A primeira colisão é perfeitamente inelástica, a segunda é perfeitamente elástica e na terceira colisão o sistema formado pelos carinhos A e B ganhou energia por trabalho.