Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação do Momento Linear

Ver Teoria
Exercício 271234567891011121314151617181920212223242526282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFF, Física 1, Prova 1, 2016.1

Um corpo de massa 3 M , movendo-se no sentido positivo do eixo-x a uma velocidade v 0 , se rompe em duas partes cujas massas são M e 2 M , conforme mostrado na figura. Determine as rapidezes finais das partes em função de v 0 .

  1. v 1 = 2 2 + 1 v 0 ; v 2 = 6 3 + 1 v 0
  2. v 1 = 3 3 + 1 v 0 ; v 2 = 3 2 3 + 1 v 0
  3. v 1 = 2 2 v 0 ; v 2 = 4 3 v 0
  4. v 1 = 3 2 3 + 1 v 0 ; v 2 = 3 3 + 1 v 0
  5. v 1 = 2 2 v 0 ; v 2 = 3 4 v 0

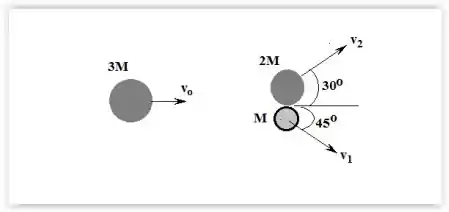
Passo 1

Essa é uma questão de conservação do momento linear bidimensional.

Por isso, vamos dividir nos dois eixos:

∆ p x = 0

∆ p y = 0

E também cada velocidade após a colisão pode ser separada em duas componentes

v → = v x x ^ + v y y ^ = v c o s θ x ^ + v s e n θ y ^

Começando pelo eixo x , temos que todas as velocidades são positivas já que estão apontando para a direita:

3 M v 0 = 2 M c o s 30 ° v 2 + M c o s 45 ° v 1

Dividindo por M

3 v 0 = 2 c o s 30 ° v 2 + c o s 45 ° v 1

Substituindo os cossenos

3 v 0 = 2 × 3 2 v 2 + 2 2 v 1

3 v 0 = 3 v 2 + 2 2 v 1

Beleza! Agora partimos para o eixo y .

Passo 2

Vamos analisar agora o eixo y :

∆ p y = 0

p f = p i

O momento inicial em y é nulo já que a partícula inicial tem velocidade horizontal.

p f = 0

Agora a partícula de massa 2 M tem velocidade na direção y positiva por que está indo para cima e a partícula de massa M tem velocidade negativa por que está indo para baixo

2 M s e n 30 ° v 2 - M s e n 45 ° v 1 = 0

Dividindo por M

2 s e n 30 ° v 2 - s e n 45 ° v 1 = 0

Substituindo os senos

2 × 1 2 v 2 - 2 2 v 1 = 0

v 2 = 2 2 v 1

Passo 3

Agora temos um sisteminha de equações. Como achamos v 2 no passo anterior basta substituir na equação que achamos no passo 1

3 v 0 = 3 v 2 + 2 2 v 1

3 v 0 = 3 2 2 v 1 + 2 2 v 1

Botando 2 v 1 / 2 em evidencia do lado direito da equação

3 v 0 = 3 + 1 2 2 v 1

Isolando v 1

v 1 = 6 v 0 2 3 + 1

Racionalizando

v 1 = 6 v 0 2 3 + 1 × 2 2 = 6 2 v 0 2 3 + 1

v 1 = 3 2 v 0 3 + 1

Passo 4

Agora vamos achar v 2 . Como

v 2 = 2 2 v 1

Basta substituir

v 2 = 2 2 3 2 v 0 3 + 1 = 3 × 2 v 0 2 3 + 1

v 2 = 3 v 0 3 + 1

Resposta

D )   v 1 = 3 2 3 + 1 v 0 ; v 2 = 3 3 + 1 v 0

Exercícios de Livros Relacionados

Dois veículos espaciais em órbita estão acoplados. A massa de um deles é de 1000 Kg e a do outro de 2000 Kg. Para separá-los, é denotada entre os dois uma pequena carga explosiva, que comunica uma ene
Vários pesquisadores em ensino de física alegam que parte da origem das concepções alternativas entre os estudantes são os efeitos especiais que eles veem em desenhos animados e em filmes. Usando a co
Uma espaçonave é separada em duas partes pela detonação dos rebites explosivos que as mantêm unidas. As massas das partes são 1200k g e 1800k g ; o módulo do impulso que a explosão dos rebites exerce
"Relativamente" é uma palavra importante. Na Fig. 9-72, o bloco E de massa m e =1,00k g e o bloco D de massa m D=0,500k g são mantidos no lugar com uma mola comprimida entre os dois blocos . Quando os
Um certo núcleo radioativo (pai) se transforma em um núcleo diferente (filho) emitindo um elétron e um neutrino. O núcleo pai estava em repouso na origem de um sistema de coordenadas x y . O elétron s