Um veículo da Ford, tipo Escort, cuja massa é , colide com um veículo de entrega, também da Ford, mas cuja massa é . A colisão acontece em um ângulo reto quando atravessam um cruzamento durante uma tempestade de neve, e a velocidade de ambos os veículos quando entram nesse cruzamento são iguais. Desprezando a força de atrito, qual a trajetória possível de ambos os veículos após a colisão?(admita que os veículos se mantenham preso um ao outro após a colisão).
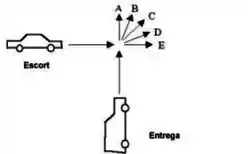
- Trajetória
- Trajetória
- Trajetória
- Trajetória
- Trajetória
Passo 1
Bem galera, o segredo aqui é analisar o vetor momento resultante de acordo com os momentos inicias.
Como vamos somar vetores, é de se esperar que o vetor resultante fique mais próximo do vetor maior.
Bom, o vetor momento linear é dado por:
Como as velocidades são iguais, o maior vetor linear será aquele que tem a maior massa, no caso, o carro de entrega.
Passo 2
Então, podemos resolver isso qualitativamente com um desenho:
E:
Então:
Assim, o vetor resultante vai ficar mais ou menos assim:
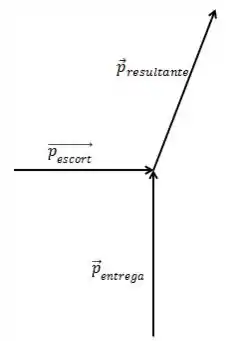
Ou seja, como a componente vertical dele é maior que a horizontal, ele vai fica mais “em pé” do que “deitado”. Isso quer dizer que, em outras palavras, que o vetor momento faz um ângulo maior que com a horizontal.
Então, o melhor vetor pra representar isso é:
Então:
b)
Resposta
b)