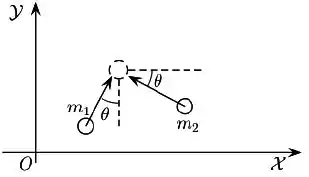
Dois corpos de massas iguais se deslocam em uma mesa horizontal sem atrito. Inicialmente eles possuem velocidades de mesmo módulo e o objeto de massa se desloca fazendo um ângulo com o eixo enquanto o de massa fazendo o mesmo ângulo , porém com o eixo , conforme a figura a seguir. Em um certo instante, os corpos colidem e passam a se deslocar juntos. O trabalho realizado pelas forças internas, que atuam durante a colisão, sobre o sistema será de:
(a)
(b)
(c) O trabalho é nulo.
(d)
(e)
(f)
Passo 1
A questão trata de uma colisão bidimensional, em que temos as massas e as velocidades iniciais. Como eles saem juntos da colisão, conseguimos encontrar a velocidade final dessas partículas.
Tá bom, mas pra que a gente quer essa velocidade final?
Tá vendo que a questão pede o trabalho das forças internas que atuam nessa colisão?
Uma boa maneira de relacionar isso com os dados que temos é através do teorema trabalho-energia cinética:
Como as forças internas são as únicas resultantes durante essa colisão, podemos dizer que o trabalho delas será realmente a variação de energia cinética do sistema:
Passo 2
Beleza, vamos achar a variação da energia cinética na colisão:
Bom, como já temos as massas e as velocidades iniciais, podemos calcular a energia cinética inicial :
Como , temos:
Passo 3
Para encontrar a energia cinética final , precisamos primeiro encontrar a velocidade final com que as partículas saem da colisão.
Então, vamos tentar analisar por meio da conservação do momento linear do sistema:
Mas como as velocidades têm umas direções meio chatas, dá uma olhada no que podemos fazer.
Passo 4
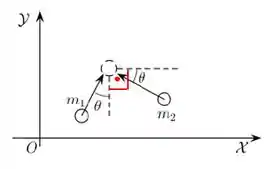
Tá vendo que esse ângulo é ?
Então, podemos dizer que esse ângulo aqui, é :
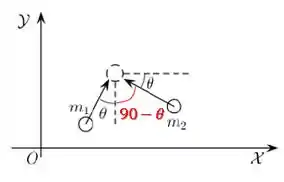
Okay, agora olha pro ângulo que as velocidades das partículas têm entre si:
Então, as velocidades das partículas fazem um ângulo de entre si.
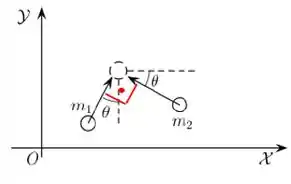
Ahh, ótimo. Então podemos fazer o nosso sistema de eixos nas direções das velocidades.
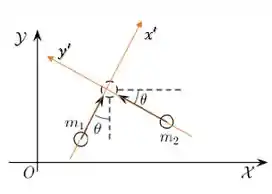
Isso vai simplificar bastante a nossa vida.
Putz, mas eu nunca ia pensar nisso na hora da prova...
Sem problemas, a gente sempre pode decompor as velocidades de cada partícula nos eixos e tradicionais usando e que vamos chegar no resultado certinho.
Passo 5
Agora que temos um outro sistema de eixos, podemos conservar o momento linear separadamente em cada um deles:
Começando com o eixo , temos apenas o momento linear da partícula 1 inicialmente, então:
Essa será a componente da velocidade final em .
No eixo , temos uma situação parecida:
Essa será a componente da velocidade em .
Ou seja, a velocidade final das duas partículas será:
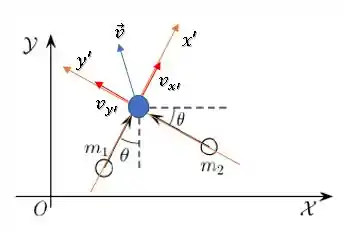
Passo 6
Agora, é só a gente achar o módulo dessa velocidade final para calcular a energia cinética final .
O módulo de será:
Já deixamos elevado ao quadrado na malandragem de calcular a energia cinética :
Passo 7
Por fim, conseguimos a variação de energia cinética :
Pronto, achamos então o trabalho das forças internas:
Resposta
Letra (a)