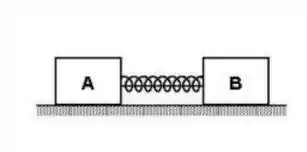
Duas caixas, da massa e , estão presas através de uma mola que está comprimida e um fio e em repouso sobre um plano horizontal com atrito desprezível, como mostra a figura. Suponha que o fio seja cortado por uma pessoa e o bloco "" passe a deslizar com uma velocidade de . Nessas condições, podemos afirmar que a velocidade adquirida pelo bloco "" vale:
(a)
(b)
(c)
(d)
(e)
Passo 1
Opa!!! Vamos lá!!
Considerando o momentos em que o fio foi cortado e em seguida, quando o bloco B tem velocidade . Temos que, nesse intervalo, não tem forças externas atuando no sistema. Então o momento linear do bloquinho se conserva!
Assim que o fio é cortado, consideramos a iminência de movimento, ou seja, as velocidades dos bloquinhos ainda são nulas. Então no início, .
Substituindo as massas:
O bloquinho B adquire uma velocidade de , então:
Maravilha!! Suave na nave?
Resposta
Alternativa (a)